与SVM算法功能一样，逻辑回归（Logistic Regression）常用于二分类，SVM是利用内积空间的超平面实现分类，逻辑回归的实现类似于神经网络，确切的说，逻辑回归是只有一个隐藏层、隐藏层只有一个节点的神经网络。逻辑回归使用交叉熵作为损失函数，曾在讨论信息熵一篇中详细介绍过，交叉熵本质上是最大似然法，两者推导出来的损失函数是一致的。

    从概率学角度来看，二分类模型样本的结果只有两类，是一个二项分布：两个互斥事件可分别用X、Y表示，事件X的概率为P(X)=p,则P(Y)=1-p。如有n个样本，X事件发生的次数等于k的概率为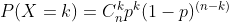：,根据中心极限定理可知，当n较大时，二项分布可以近似于标准差为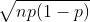，数学期望为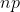的正态分布，即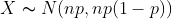，正态分布的概率分布函数是一个递增函数，如下图所示：

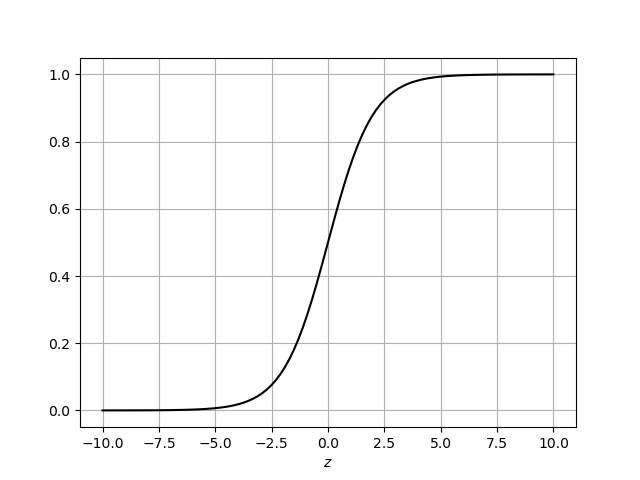
正态分布的概率密度函数是一个钟形，如下图：

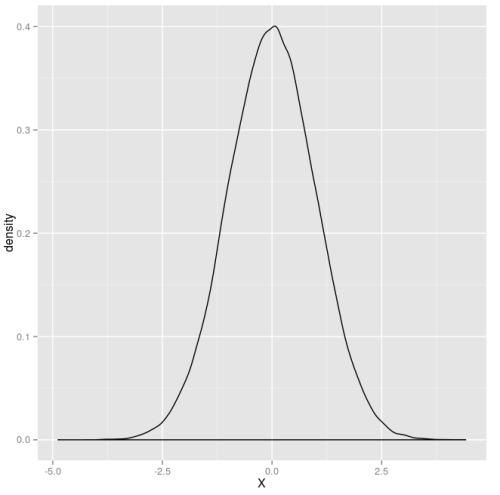
 逻辑回归用Sigmoid函数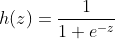：来模拟正态分布概率函数，求导h(z)可得概率密度函数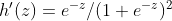：，导数函数h'(z)图像如下：

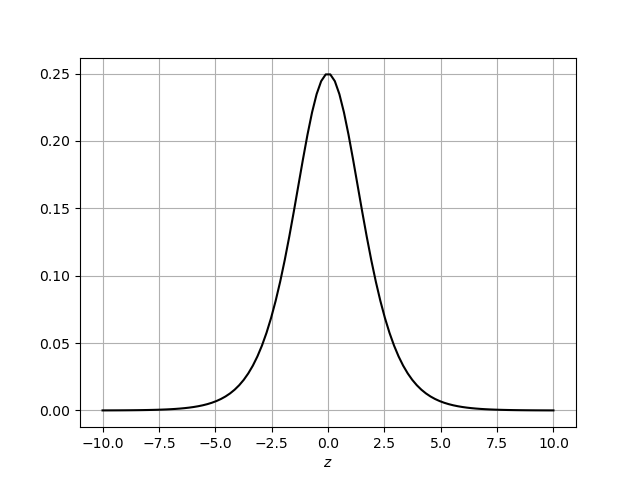
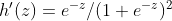与正态分布的概率密度函数非常相似的，公式中z是一个实数。假设样本数据有n个特性，即x∈R^n，利用逻辑回归实现分类时，需设定一组参数θ，θ∈Rⁿ，通过内积运算z=θ^Tx,将高维属性数据变成一个实数，将z代入h(z)后得到每一个样本发生的概率，逻辑回归目的是求出参数θ， 与SVM算法一样，当样本数据线性不可分时，z=θ^Tx并不能将样本数据映射为两个不相交的凸集，这种情况下需要使用核函数K(x)将样本数据先变为可分集。

一、最大似然法求参数

    样本数据共有m个，第i个样本为(x_i,y_i),当y_i=1时，代表发生随机事件X，代入概率分布函数有：

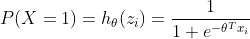                                    (1.1)

而当y_i=0时，代表发生事件Y，可以用P(Y=1)或P(X=0)表示，因此有关系式：

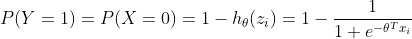     (1.2)

(1.1)和(1.2)分别对应样本为不同分类时概率，可由通用公式表示：

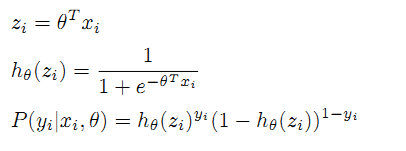
根据上面的公式表，可得到最大似然法的目标函数：

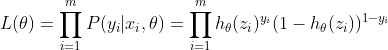
取L(θ)对数，得到等效的目标函数l(θ):

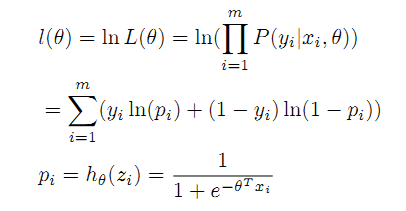
求函数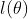最大值即可得到参数θ值,这里将函数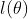处理一下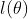，除以-1/m,求函数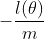最小值与求函数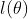最大值是是等效的：

对公式(2)求各个未知分量偏导数，偏导数为0时解方程可得到参数向量θ最优值。对函数F(θ)之前，先来看下Sigmoid函数的导数性质：

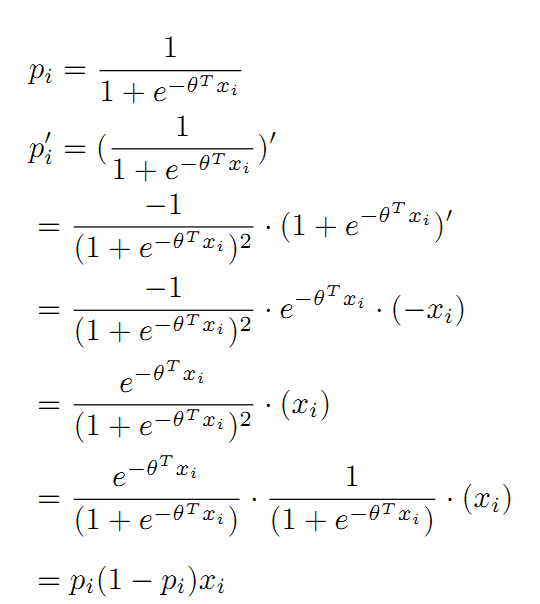
 根据上式 可求出：

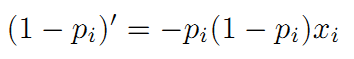
可以看出Sigmoid函数的导数有较好的规律性，可以用上面两个公式对F(θ)求导数：

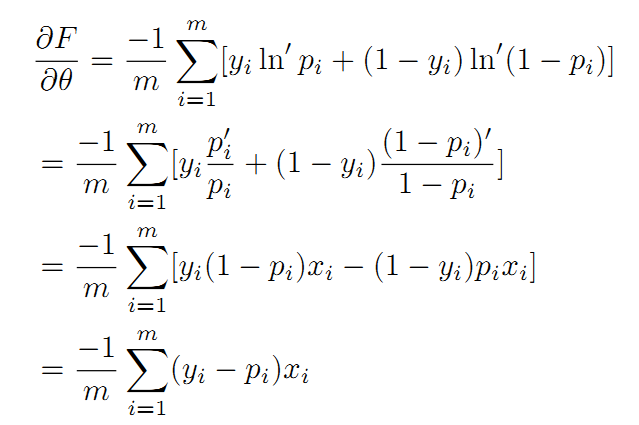
利用上式求θ中第j个分量的偏导数：

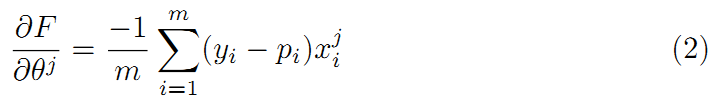
接下来根据以上的推导过程，用代码实现逻辑回归功能，下例使用的数据集是鸢尾花数据，鸢尾花数据可以分为三类，分别是山鸢尾 ，北美鸢尾，变色鸢尾；鸢尾花具有4个属性，分别是花萼的长度、花萼的宽度、花瓣的长度，花瓣的宽度。基于本篇是二分类，程序只加载了山鸢尾 ，北美鸢尾两类数据。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.datasets import make_blobs
import  math
stepLowerlimit=1e-5
def logexp(v):
    return math.log (v,math.e)
#Sigmod函数 计算概率
def probility(x,w):
    #print('内积:%0.4f'%(-np.dot(x,w)))
    return 1/(1+math.e **(-np.dot(x,w)) )

#只含有步长的一元函数
def stepfun(w, g,  x,y,step ):
    value=0
    ws=w-g*step
    for i in range(x.shape[0]):
        if y[i]==1:
            value=value+logexp(probility(x[i,...],ws)  )
        else:
            value = value + logexp(1-probility(x[i, ...], ws) )
    return  -value/x.shape[0]

#试探法求步长系数
def explore618step(w, g,  x,y ):
    r=np.array([[0,10]],dtype=np.float)
    alpha=0.618
    l=1e-5
    a,b,iterNum=r[0,0],r[0,1],0
    #shrinkDirection=1代表右端缩减，shrinkDirection=0代表左端缩减
    shrinkDirection=None
    while b-a >l:
        if shrinkDirection==None:
            lambda_k = a + (1 - alpha) * (b - a)
            mu_k = a + alpha * (b - a)
        if shrinkDirection==1:
            mu_k=lambda_k
            lambda_k = a + (1 - alpha) * (b - a)
        if shrinkDirection==0:
            lambda_k=mu_k
            mu_k = a + alpha * (b - a)
            pass
        s1=stepfun(w, g,  x,y,lambda_k )
        s2 = stepfun(w,   g,   x, y, mu_k )
        if s1<=s2:
            a,b,shrinkDirection=a,mu_k,1
        else:
            a, b ,shrinkDirection= lambda_k, b,0
    step=(b+a )/2
    return step
#逻辑回归实现
def lgr(w,x,y,counter):
    #梯度
    g=np.zeros([x.shape[1]])
    for i in range(y.shape[0]):
        for j in range(x.shape[1]):
            g[j] = g[j] + (y[i] - probility(x[i, ...], w)) * x[i, j]#公式2
    g =-g /y.shape[0]
    distance = math.sqrt(np.dot(g,g.T) )
    g = g  / distance
    step = explore618step(w,  g,   x, y )
    for j in range(x.shape[1]):
        w[j] = w[j] - g[j] * step
    if (step <= stepLowerlimit):
        return w,counter
    else:
        counter=counter+1
        return lgr(w,x,y,counter )

def check(w,x,y):
    correctNum=0
    totalNum=0
    for i in range(x.shape[0]):
        p=probility(x[i, ...], w)
        if (p>0.5 and y[i]==1):
            correctNum=correctNum+1
        if (p<0.5 and y[i]==0):
            correctNum=correctNum+1
        totalNum=totalNum+1
    print('正确=%d 总数=%d'%(correctNum,totalNum))
#加载数据集
def loadDataSet():
    iris = datasets.load_iris()
    X = iris['data']
    Y = iris['target']
    x = X[Y != 2]
    y = Y[Y!= 2]
    return x,y

if __name__=='__main__':
    x, y = loadDataSet()
    w = np.zeros(x.shape[1], dtype=np.float)
    w,c = lgr (w, x.copy(), y.copy(),0)
    print('迭代次数=%d'%(c) )
    print('参数',w )
    check(w,x,y)

加载数据集合后利用梯度下降法，求解损失函数F(θ)的最小值，前面已经分析过，F(θ)描述的是交叉熵。求梯度时过程中代码

g[j] = g[j] + (y[i] - probility(x[i, ...], w)) * x[i, j]

是利用公式(2)的推导的结果得到各个参数分量的梯度，得到梯度后利用0.618一维搜索法（一维搜索参考本站文章一维搜索），获得步长系数，程序退出的条件是步长系数小于阈值，代表已经到达最值点，代码运行结果如下图：

二、正则化解决过拟合问题

    上面的逻辑回归模型是基于训练集，在实际分类时往往不具备泛化能力。介绍决策树时，决策树的去拟合是通过剪枝操作完成的，逻辑回归实现去拟合方法是降低参数的绝对值，参数绝对值大意味着模型偏向于某些属性，这种偏好是为了迎合训练集的数据特征，逻辑回归去拟合目的就是为了消除这种偏好。

    另外，从概率学角度来说，二项分布要用正态分布近似时，有一个隐含的条件：二项分布发生某一个事件时，造成该事件发生的因素可能有多个，正态分布要求在众多因素中，每一个因素都不能起决定性作用。在逻辑回归中，因素可以理解为样本的属性，每一个因素都不能起决定性作用意味着模型不能偏好某一属性，换句话说，所有属性分配权重需均匀。观察上面代码实现的逻辑回归模型，参数绝对值为：11,17,38,21，显然模型是有偏好的，说明模型有过拟合的倾向。

    逻辑回归是利用正则化手段实现去拟合、泛化的功能，正则化的实现借鉴了惩罚函数的思想，具体做法是把参数向量的模、或者称范数，加入到目标函数中，最小化目标函数过程中，要求同时减小参数向量的范数，从而实现降低对某些属性的偏好。根据采用范数的形式，逻辑回归常用的有L1正则化与L2正则化。

2.1  L1正则化

    L1正则化采用了L1范数，即 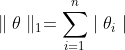,L1范数与目标函数结合生成一个新的目标函数：

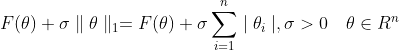
σ称为惩罚因子，在惩罚函数一节中介绍外点惩罚函数法时曾说过，通过增大σ值可使得向量范数不断变小。具体过程为：初始化参数σ，求目标函数最小值，然后增大增大σ值，直到惩罚项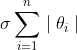小于某个阈值时，退出计算得到目标参数。

    L1正则化特点是参数比较稀疏，即参数向量中有大量的参数为0，F(θ)与惩罚项函数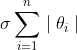的等值线如下图所示：

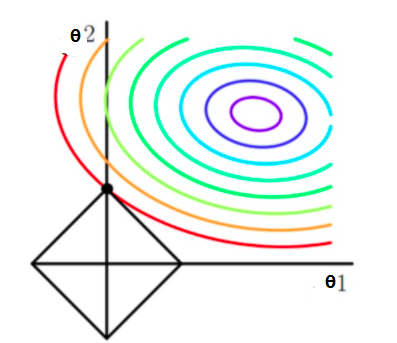
圆形曲线是函数F(θ)等值线，正方形是惩罚项函数的等值线，没有加入惩罚项时，F(θ)的最小值可在等值线中心紫色处；加入惩罚项后，需要兼顾惩罚项数值，即正方形的边长不能太长，因此这时不能再取原中心处作为最优解。上图可看出，L1正则化倾向于将正方形的顶点处作为最优解，由于顶点同时也在坐标轴上，取最优解时有部分参数为0，即L1正则化最后得到是稀疏的参数向量。

    前面介绍过，逻辑回归利用了中心极限定理，利用正态分布近似二项分布时，需要参数均匀的小，L1正则化对于逻辑回归而言，效果不是非常好，推荐使用L2正则化实现逻辑回归的泛化过程。

2.2  L2正则化

    L2正则化使用范数形式为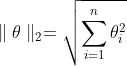：,与目标函数结合为新函数：

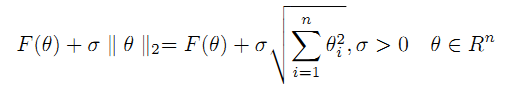
L2范数很好理解，它代表到原点的距离，或称为模， F(θ)与惩罚项函数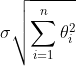的等值线如下图：

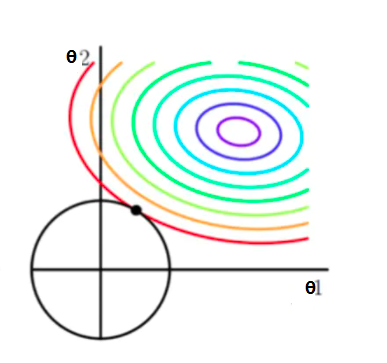
惩罚项函数等值线可想象为一个圆周，取得最优解时，圆周与F(θ)函数等值线相切于一点，可以看出相比L1正则化，有两点不同：一是L2正则化获得最优解时，各个参数都均匀的小，不会像L1正则化那样将部分参数变为0，L2正则化这个特性是符合逻辑回归需求的；第二个不同是，L1正则化F(θ)的等值线可能会与正方形等值交于一条边的两个顶点，这就造成L1正则化的最优解往往是多个，而L2正则化等值线相切于一点，最优解通常只有一个。

    L1正则化与L2正则化只是选择了不同的范数，核心思想与形式都是一致的，代码实现上区别也不大，本篇介绍L2正则化实现过程，在L2正则化基础上稍加改动即可变为L1正则化，将之前例子加上L2正则化后代码如下：