一维搜索
求解一元函数的最值过程称为一维搜索,本篇以求函数最小值为例。一元线性函数可以通过单纯形法获得最小值,所以在实践中如果需要使用一维搜索,这个一元函数通常是一个至少有二阶导数的曲线函数。一维搜索典型的应用是步长系数的确定,如利用梯度下降法求解函数最小值时,获得函数在可行点的梯度后,需要先将梯度向量取反然后乘以一个步长,这个步长不能太小,太小对于算法收敛速度太慢;也不能太长,太长会造成在极值点附近时穿越最值点,导致算法在极值点附近震荡。为了求一个合理的步长系数,通常把可行点沿着某一个方向乘以一个步长系数,延伸得到新的可行点,将新的可行点带入目标函数求最小值,此时目标函数除了步长系数之外都是常量,目标函数变为以步长为变量的一元函数,求解该一元函数最小值就可以得到最优的步长系数。
一维搜索根据目标函数的不同,选择策略也灵活多变,按算法特性大致可以分为两类,一类称为试探法,试探法是利用最小值是一个‘谷底’,试探着用一个不断缩小的范围最后锁定谷底得到最小值;另一类算法叫做函数逼近法,函数逼近法用一个函数像尺子一样逼近目标函数其中一部分,通过尺子函数得到这部分的最小值后,同时得到目标函数下一个需要求最小值的片段,周而复始不断迭代后,新生成的尺子函数会越来越逼近目标函数最低点,最后当误差在一定范围内时,直接求解尺子函数的最小值即为目标函数的最小值。
在介绍一维搜索算法之前先来介绍下凸函数的概念,介绍单纯形法时曾详细介绍过凸集,凸函数的定义与凸集相似,具体定义为, f(x)是定义在 凸集S上函数,如果凸集S上任意的x,y都有:
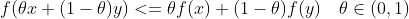
则称f(x)为凸函数,从图像上来看凸函数像一个碗,这个函数只有一个谷底,有时候也称这样的函数叫单峰函数:
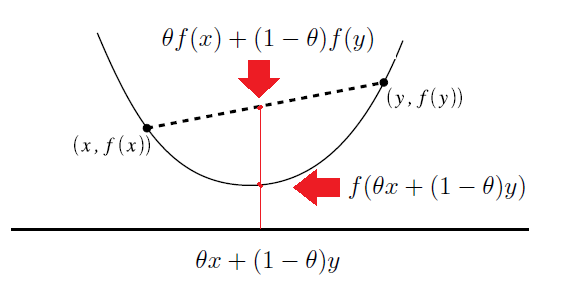
使用一维搜索时我们希望目标函数在定义域内是一个凸函数,或者在某一个区间内是一个凸函数,这样得到最小值是唯一的,当目标函数有多个谷底时,比如下面这个函数,一维搜索只能得到一个局部最小值。
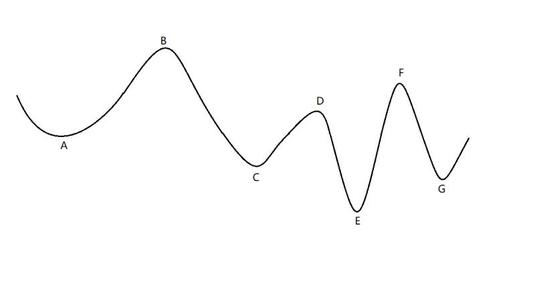
一、试探算法:0.618法
设一个在[a1,b1]上的凸函数f(x),并设误差系数e和缩短比例系数α(0<α<1),在初始区间[a1,b1]内取一个对称的子区间[λ1,μ1],对称含义是指λ1到端点a1的距离等于μ1到端点b1的距离,为满足对称性可以这样构建λ1、μ1:设λ1到端点b1的距离是区间[a1,b1]长度的α倍,μ1到端点a1的距离也是区间[a1,b1]长度的α倍,效果如下图所示:
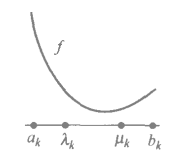
得到λ1、μ1位置后将λ1、μ1带入目标函数后,会有以下两种情况:
情形一:f(λ1)<=f(μ1),这时将区间原端点b1设为μ1,a1依然保持不变,这时得到新的区间[a2,b2]=[a1,μ1],此时新区间的长度缩短为原区间[a1,b1]长度的α。检查新区建长度μ1-a1,如果长度小于e则退出计算,这时最小值点为(μ1+a1)/2;如果大于误差系数e,则在新的区间[a1,μ1]再次取一个对称子区间[λ2,μ2],λ2、μ2选择的规则与初始时一样,即λ2到b2的距离是区间[a2,b2]长度的α倍,μ2到端点a2的距离是区间[a2,b2]长度的α倍。
情形二:f(λ1)>f(μ1),这时将区间原端点a1设为λ1,b1保持不变,这时得到新的区间[a2,b2]=[λ1,b1],检查新区建长度b-λ1,如果长度小于e则退出计算,此时有最小值(λ1+b1)/2;如果大于误差系数e,则在新的区间[λ1,b1]再次取一个对称子区间[λ2,μ2],[λ2,μ2]区间设置规则与情形一相同。
当新的子区间[ak,bk]距离大于误差e时,说明范围还没缩小到合理的区间内,这时需要将新生成子区间进一步切分得到区间[λk,μk],并将λk、μk再次带入目标函数计算,随后根据以上两种情形进行判断,直到距离小于误差e时退出计算。由于每次生成的子区间[ak,bk]是不断缩小的(0<α<1),算法最终能保证收敛于函数最小值点。另一方面,在算法实现中每次都是选择函数值较大一方缩短距离,就好比一个物体的重心偏向函数值较大一方,选择函数值较大一方缩短就能保证重心逐渐向最小值点靠近。从图像上来看,新的区间范围一直能覆盖函数谷底部分,每次生成的区间是一个子套区间,根据闭区间套定理,不断缩小的套区间极限是一个点,即最小值点。
每次缩短的比例α为0.618时称为0.618法,我们知道0.618是一个黄金比例,α设为0.618时有什么特殊功效吗?假设在第k次迭代计算时得到新的区间[ak,bk],随后生成一个内部子区间[λk,μk],根据子区间对称性、缩短的比例α可以得到以下两个等式:
bk-λk=μk-ak
bk+1-ak+1=α(bk-ak) ⑴
这样可以得到λk、μk的表达式:
λk=ak+(1-α)(bk-ak)
μk=ak+α(bk-ak) ⑵
1)此时如果有f(λk)<=f(μk),根据算法特性可以知道下一次新区建间为:
[ak+1,bk+1]=[ak,μk]
同时需要在[ak+1,bk+1]内要得到检查点[λk+1,μk+1],从方程组⑵知道:
μk+1=ak+1+α(bk+1-ak+1) =ak+α(μk-ak ) =ak+α2(bk-ak )
如果恰好有:
μk+1=ak+α2(bk-ak ) =ak+(1-α)(bk-ak) = λk ⑶
即μk+1=λk时,则新的μk+1不需要计算,只要取上一轮的λk即可,而要满足方程 ⑶则是要满足一元二次方程:
α2=1-α
由于要求α>0,解上面这个方程可以得出α=0.618
2)当f(λk)>f(μk),同样可以得到这样结论,当α=0.618时,λk+1不需要计算,只要取上一轮的μk即可。
由此可见,如果选择α=0.618,在每轮迭代获得检查点λ、μ时,其中一个参数一定可以取自上轮的参数,这样一来可以节省很多计算。将上述算法编制程序如下,这是利用0.618试探法求函数f(x)=2x2-3x-1最小值的python代码:
import numpy as np
#试探法求解f(x)=2x^2-3x-1最小值
def explore618():
r=np.array([[-2,2]],dtype=np.float)
alpha=0.618
l=1e-5
a,b,iterNum=r[0,0],r[0,1],0
#shrinkDirection=1代表右端缩减,shrinkDirection=0代表左端缩减
shrinkDirection=None
while b-a >l:
if shrinkDirection==None:
lambda_k = a + (1 - alpha) * (b - a)
mu_k = a + alpha * (b - a)
if shrinkDirection==1:
mu_k=lambda_k
lambda_k = a + (1 - alpha) * (b - a)
if shrinkDirection==0:
lambda_k=mu_k
mu_k = a + alpha * (b - a)
if(2*lambda_k**2-3*lambda_k-1)<=(2*mu_k**2-3*mu_k-1):
a,b,shrinkDirection=a,mu_k,1
else:
a, b ,shrinkDirection= lambda_k, b,0
pass
iterNum = iterNum + 1
x=(b+a )/2
return x,2*x**2-3*x-1,iterNum
if __name__ == '__main__':
x, y,iterNum = explore618()
print('试探法 在%.2f处最小值%.2f 迭代次数%d' % (x, y, iterNum))程序还是非常简单,通过shrinkDirection变量得到上一轮缩短的方向,同时根据0.618法特性,可以复用上一轮的参数,代码运行结果如下:

二、函数逼近法
函数逼近法是使用一个'尺子函数'逼近目标函数的一个片段,利用尺子函数得到这一片段的最小值后,取尺子函数最小值点作为需要迭代的下一个片段,依次重复,最后尺子函数最小值会收敛于域目标函数的最小值点。可以把每个片段尺子函数可以理解为目标函数空间的基,用多个尺子函数逼近目标函数的过程可以理解为用多个基来拟合目标函数,在调和分析中有一种方法叫小波分析,通过伸缩信号的尺度来拟合目标信号,他们所用的思想都是一样的。函数逼近法有很多种,常用的牛顿法、二次函数逼近法、抛物线法、插值法等,这些算法的核心思想都可以用下面的图来说明:

上图f(x)是目标函数,首先构建一个尺子函数s1(x)与目标函数相切于一点x0,求出函数s1(x)最小值点为x1,在x1处再构建一个函数s2(x),使函数s2(x)与目标函数相切于点x1,求出函数s2(x)最小值点x2,不断迭代后可以在第k步得到函数sk(x),函数sk(x)最小值收敛于目标函数的最小值。
| 上一篇 Bagging集成算法 | 下一篇 KKT条件 |
| 评论区 | |