K-Means算法是一种无监督算法，不用标注分组信息即可完成模型的训练，K-Means算法思路清晰、使用简单，是一种高效聚类算法，其核心思想是利用距离函数,将属性相似的样本数据尽量聚集成一个集合，称每个集合为一个簇，同时要让不同簇之间的差异尽量的大。

一、K-Means算法介绍及实现

K-Means算法首先设定k个分类，假设样本的数据个数为N,具体步骤如下：

1）任选样本中k个点作为k个簇的质心(重心)，如有μ₁、μ₂、μ₃、...,μ_k。

2）计算每个样本与μ₁、μ₂、μ₃、...,μ_k的距离，常见的距离函数有欧氏距离、曼哈顿距离、闵可夫斯基距离等；如第j个样本点y_j与质心u_i（i<=k）之间距离最短，则将y_j归为i类，保存y_j的分类i。

3）遍历每个样本点,将每个样本点按本轮分类分别以向量形式累加后，除以每个分类的个数，得到新的质心，计算公式如下：

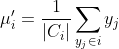
4）将新的质心与本轮初始质心比较，当两者误差小于一定阈值后退出计算，得到最终的分类质心，否则重复第2)步。

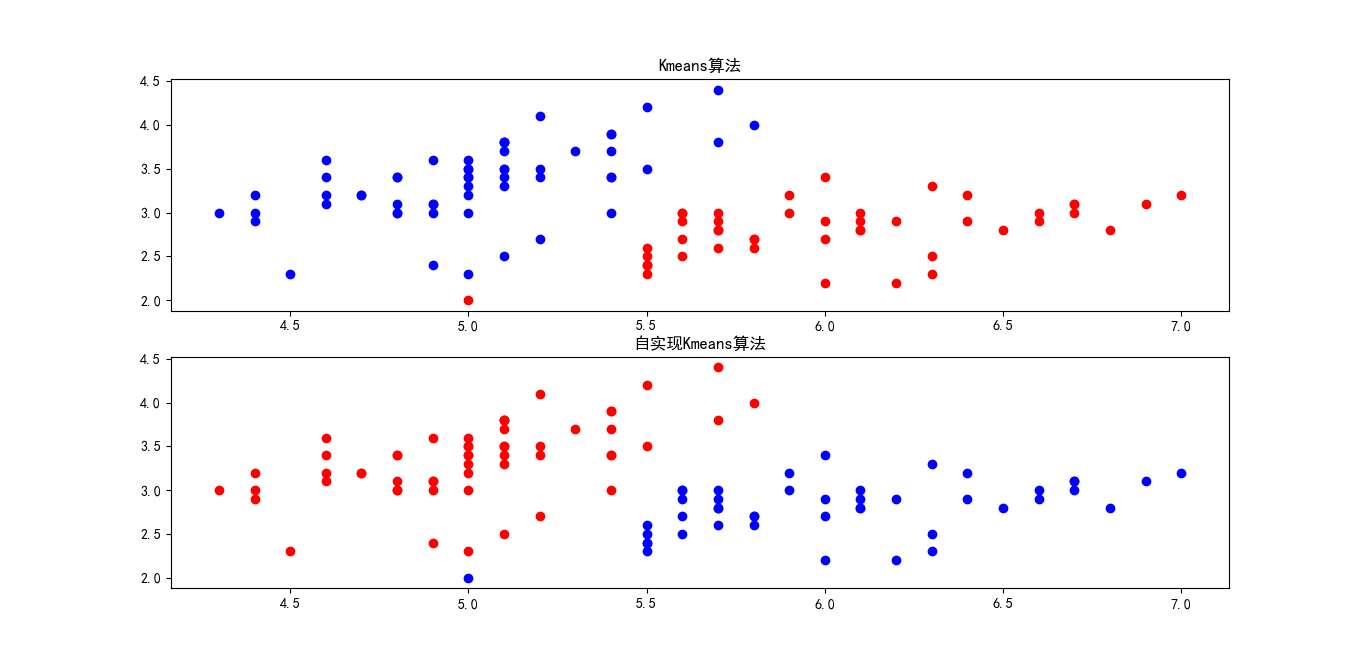
下面以鸢尾花数据为例，分别用系统自带的K-Means算法与自实现的代码比较，为了演示方便，选择了鸢尾花数据中的两个分类。

import numpy as np
from sklearn.cluster import  KMeans
from sklearn.datasets import  load_iris
import  matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
colors=['b','r','y']
ERROR=1e-5
def load():
    #加载鸢尾花数据，为方便二维演示只加载两类
    data = load_iris()
    classOne = np.where(data["target"] == 0)
    classTwo = np.where(data["target"] == 1)
    v=np.concatenate((data["data"][classOne,:2],data["data"][classTwo,:2]),axis=1)
    return np.squeeze(v)

#计算两个向量欧氏距离
def getdistance(v1,v2):
    v=v1-v2
    return  np.dot(v,v.T)

#KMeans实现
def KMeansNew(data,k1=None,k2=None):
    if(k1 is None or k2 is None  ):
        k1, k2 = data[0, :-1], data[1, :-1]
    for d  in range(data.shape[0]):
        d1=getdistance(data[d,:-1],k1 )
        d2 =getdistance(data[d,:-1],k2)
        data[d,2] = (0 if d1<d2 else 1)
    #计算新聚类集合质心
    u1,u2=np.zeros([1,2]),np.zeros([1,2])
    k1count,k2count=0,0
    for d in range(data.shape[0]):
        if(data[d,2]==0):
            u1[0, :]=u1[0,:]+data[d,0:-1]
            k1count=k1count+1
        else:
            u2[0, :]= u2[0,:] + data[d, 0:-1]
            k2count = k2count + 1
    newk1, newk2 =  u1[0, :]/k1count, u2[0, :]/k2count
    #小于设定阈值后从递归函数返回
    if(getdistance(newk1,k1)<=ERROR  and getdistance(newk2,k2)<=ERROR):
        return data
    else:
        return  KMeansNew(data, newk1, newk2)

def KmeansSystem(data:np.ndarray,n_clustersnumber):
    model = KMeans(n_clusters=n_clustersnumber, init='k-means++')
    model.fit(data)
    lables = model.labels_
    return  lables

def testKmeans():
    data = load()
    datacpy = data.copy()
    datacpy = np.insert(datacpy, 2, 0, axis=1)
     # 自定义KMeans
    datanew=KMeansNew(datacpy)
    #自带KMeans++实现
    lables=KmeansSystem(data,2)
    plt.subplot(211)
    for i in range(data.shape[0]):
        plt.scatter(data[i, 0], data[i, 1], c=colors[lables[i]], marker='o')
    plt.title('Kmeans算法')
    plt.subplot(212)
    for i in range(datanew.shape[0]):
        plt.scatter(datanew[i, 0], datanew[i, 1], c=colors[ int(datanew[i,2])  ] , marker='o')
    plt.title('自实现Kmeans算法')
    plt.show() 

if __name__=='__main__':
    testKmeans()

计算结构如下图：

二、K-Means++算法

K-Means算法初始时任意选择k个样板点作为质心，这导致后期更多次数的迭代，K-Means++算法改进了对初始质心的选择，通过计算，选择最为接近目标分类质心的位置作为初始质心，得到初始质心后接下来的算法与K-Means算法一致，初始质心的计算步骤如下：