本文可作为线性代数实现线性回归的下篇,先简单回顾一下，线性代数实现线性回归中介绍了子空间的概念，把子空间想象成一个超平面，子空间中任意一个向量都可以用子空间的基线性组成，实现线性回归原理是利用超平面外的一个向量与该向量在子空间里投影距离最短，或者说误差最小，求出向量在子空间的投影即可得到未知参数。

    上篇中介绍的线性空间是由实数向量组成，本文将拓展子空间的概念，空间的元素是函数称之为函数空间，函数空间里面有我们熟悉的各种函数以及这些函数的线性组合，比如三角函数可以组成一个子空间，由数学分析知道利用三角函数可以实现傅里叶变换，将其他函数表示为三角函数线性组合成的级数形式。本文中选取的空间是一个多项式空间，即其空间里基是诸如x⁰,x¹,x²,x³,...xⁿ...等多项式，目标是将其他形式函数投影到多项式函数空间里，从而得到任意函数的多项式近似表达式。

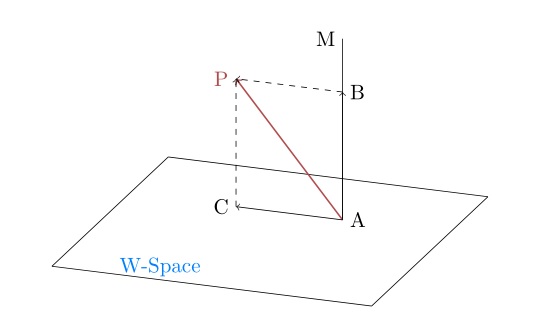
    使用上图来说明函数空间，AP代表了函数空间里的一个函数，而下面的平面代表了多项式子空间，AP在多项式空间里的投影AC代表与AP误差最小的多项式，而AC是x⁰,x¹,x²,x³,...xⁿ等多项式的线性组合，我们目标就是求出这个线性组合表达式中每个基前面的系数(坐标)。

一、一元多项式逼近任意一元连续函数

    这里结合一段python代码说明，这段代码的功能是利用多项式逼近函数f(x)=sin(x)-3cos(x)。 

import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
NSplit_Num = 10000
class polynomialAppro(object):
    def __init__(self, split=1000):
        self.splitnum = split 

    def genfunction(self):
        ar = []
        t = np.linspace(-math.pi, math.pi, self.splitnum)
        for x in t:
            ar.append(math.sin(x) - 3 * math.cos(x))
        sx = np.expand_dims(np.asarray(ar), 0)
        return sx

    def genpolynomialdata(self):
        ar = []
        t = np.linspace(-math.pi, math.pi, self.splitnum)
        for x in t:
            ar.append([1, x, x ** 2, x ** 3, x ** 4, x ** 5])
        polynomialdata = np.asarray(ar)
        return polynomialdata

if __name__ == '__main__':
    appro = polynomialAppro(NSplit_Num)
    sx = appro.genfunction()  # 1.1
    b = sx.T  # 1.2
    A = appro.genpolynomialdata()  # 1.3
    ATAminus = np.linalg.inv(np.dot(A.T, A))  # 1.4
    coordinate = np.round(np.dot(ATAminus, np.dot(A.T, b)), 4)  # 1.5
    # 打印图像验证
    x = np.linspace(-math.pi, math.pi, NSplit_Num)
    y_x = coordinate[0]+ coordinate[1] * x + coordinate[2] * (x ** 2)+  coordinate[3] * (x ** 3) + coordinate[4] * (
            x ** 4) + coordinate[5] * (x ** 5)
    plt.figure()
    plt.subplot(121)
    plt.title('原函数图像')
    plt.plot(x, b[..., 0])
    plt.subplot(122)
    plt.title('多项式逼近的函数图像')
    plt.plot(x, y_x)
    plt.show()

来看下模拟的效果图:

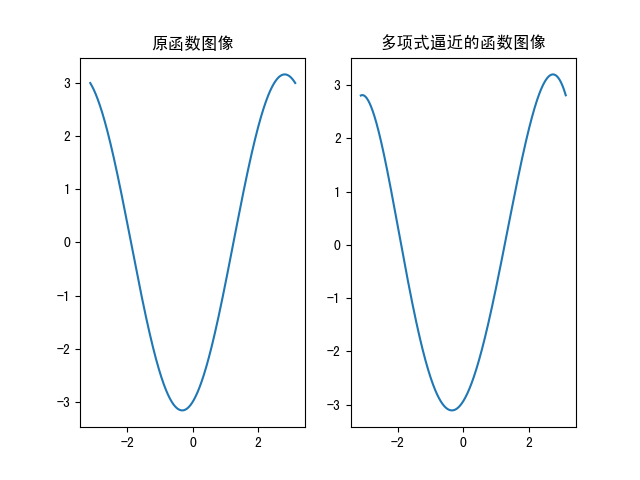
可以看到利用线性回归求出的多项式函数可以较好的逼近目标函数f(x)=sin(x)-3cos(x)，下面就代码中标注释部分说明：

#1.1 sx=appro.genfunction()

得到目标函数f(x)=sin(x)-3cos(x)在-π ，π之间的数据，将其离散化变成计算机可以处理的向量形式，本篇采用了利用显式函数生成数据，真实的应用中可能并不知道目标函数形式（如果知道具体的函数形式就不需要用多项式来近似了），sx是采集来样本数据，我们目标是通过数据计算出符合样本特征的多项式函数。

#1.2 b=sx.T

为了后期处理方便，将其处理成10000*1的向量形式。

#1.3 A=appro.genpolynomialdata()

选取x⁰,x¹,x²,x³,x⁴,x⁵作为子空间的基，并将其向量化，这里将得到一个10000*6的矩阵，此时A就是在介绍线性回归问题时的子空间。这里将函数空间元素赋值，使一个函数空间问题变为一个线性代数问题，这种离散化数据手段在计算机处理中会经常使用。

#1.4、1.5 

ATAminus=np.linalg.inv( np.dot(A.T,A))

coordinate= np.round(np.dot(ATAminus,np.dot(A.T,b)),4)

经过前面离散化处理，此时问题就变成利用线性空间求解线性回归问题，#1.4、1.5 是求出函数f(x)=sin(x)-3cos(x)在多项式子空间上的投影，这个处理过程 在之前已经讨论过，这里再复盘一遍。

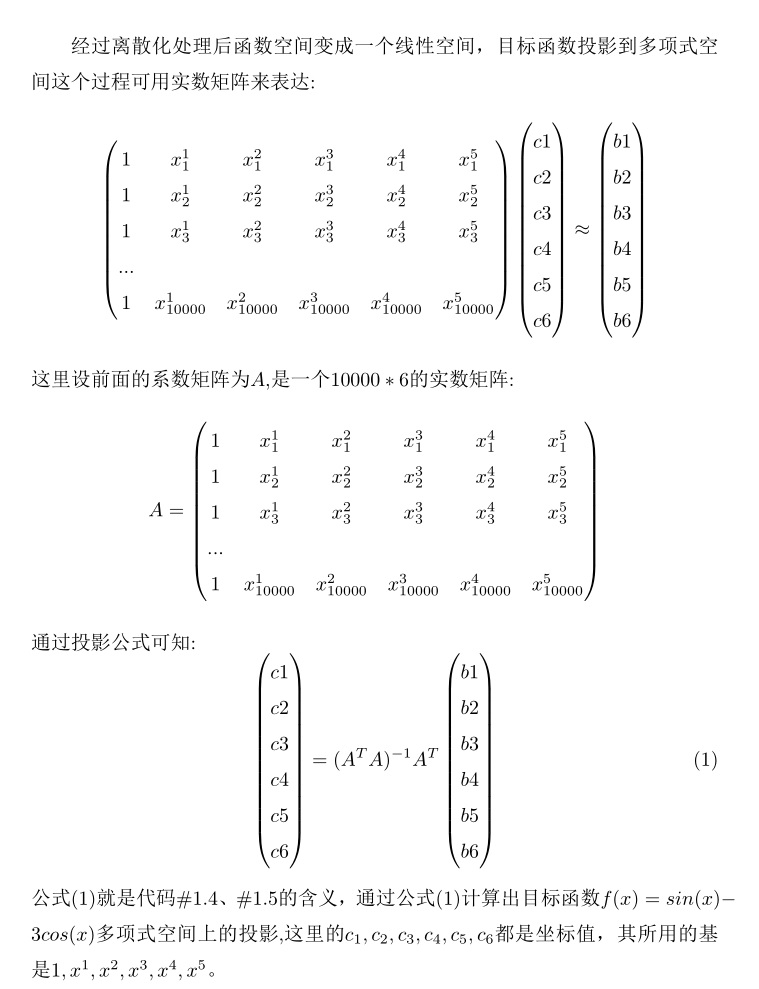
二、 二元多项式逼近任意连续二元连续函数

    二元乃至多元多项式逼近任意连续函数与一元函数类似，都是最终转化为实数矩阵形式，然后利用公式(1)求解系数，只不过在构造多项式形式上略有不同，掌握二元多项式逼近问题即可推广至任意元函数的情形，这里还是先展示一段python代码，下面代码用多项式逼近二元函数f(x,y)=sin(x)-cos(y)图像：