循环神经网络常用来做时序分析，即根据现有的按发生顺序排列的数据来预测未来的走势，循环神经网络大量用于语音分析、语言翻译、金融分析、内容推荐等领域，循环神经网络是一个大的分类，代表模型是RNN（循环神经网络）、LSTM（长短时记忆网络）,与之前介绍的全连接神经网络、卷积神经网络不同，循环神经网络在反向传播时不仅有层与层之间传递，还有时间维度上的传递。

一、RNN循环神经前向传播

     RNN是初级的循环神经网络，训练过程中每个序列中中间运算结果会进入下一次的输入中，其示意图如下：

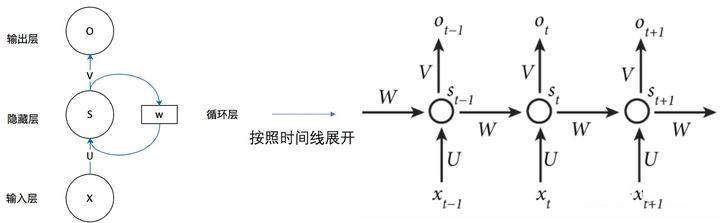
上图左边是RNN结构图，右侧是RNN按序列输入展开后的示意图，图中x_t-1、x_t、x_t+1代表一串序列，序列中每个元素都为向量，例如有编号为d₁,d₂,d₃,d₄,d₅,d₆...采集数据，每个编号数据为一个实数,可将编号d₁,d₂数据合并为一个二维向量，将编号d₃为标签值得到一个样本x₁=(d₁,d₂),y₁=d₃,依此类推，有序列x₂=(d₂,d₃),y₂=d₄、x₃=(d₃,d₄),y₃=d₅、x₄=(d₄,d₅),y₄=d₆等，采用循环神经网络类似于英语中完形填空题，我们通过语法学习培养出语感后（模型训练），可在缺失处填写正确的单词使得语句完整。

    RNN有类似全连接神经网络的隐藏层，RNN可以有多个隐藏层，以只有一个隐藏层的RNN为例，RNN前向传播的公式有：

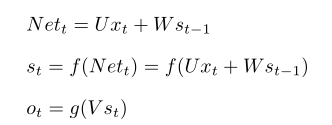 ⑴

Net_t表示序列中第t个序列的输入，对应于上图Net_t是隐藏层神经单元s的输入值，Net_t中含有上一次隐藏层的输出值s_t-1，Net_t经过激活函数f处理后为隐藏层的输出值，这个流程与全连接神经网络是很相似的，假设激活函数f选择使用双曲正切函数tanh(x),tanh(x)函数形式以及图像分别如下：

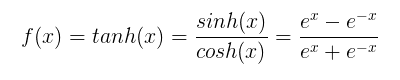
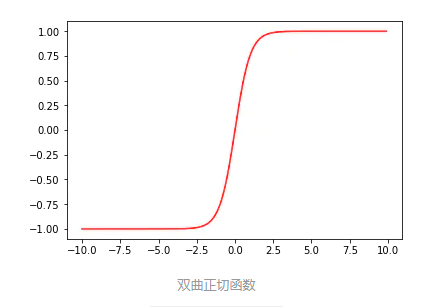
双曲正切函数导数与自身有一定形式上关联，导数公式如下：

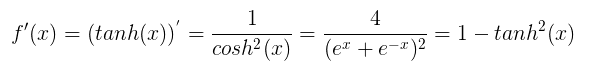
隐藏层输出乘以权重V后经激活函数g处理后变为最终RNN神经网络的输出，输出后的值根据具体问题选择适当的损失函数，如是分类问题常用交叉熵函数，与此同时激活函数g一般是softmax函数；如果是回归问题，则损失函数可选择平方误差函数，这时激活函数一般可选择Relu函数。

二、 RNN反向传播过程

2.1、循环神经网络误差梯度按时间、空间传递

    前面已经说过，循环神经网络与全连接神经网络、卷积神经网络最大不同在于误差体现时间维度上累积，这是所有包括LSTM在内所有循环神经网络的特性，通过研究RNN可以将一些结论拓展沿用到LSTM上，这正是研究RNN的意义所在。循环神经网络上反向传播时，首先要求出在时间维度上的误差梯度，然后再考虑层与层之间误差梯度传递。

    RNN实质是个全连接神经网络，可利用DNN反向传播方法推导出RNN在t时刻的误差梯度，所有神经网络都一样误差都是定位到输入端，设t时刻梯度为:

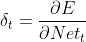
已知t时刻误差δ_t后，上一个时刻t-1的误差梯度δ_t-1根据链式求导法则有：

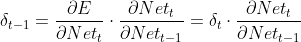 （2.1）

求δ_t-1核心是求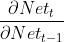_，Net_t和Net_t-1都是向量，其中有s_t-1=f(Net_t-1)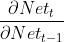，等于以下等式：

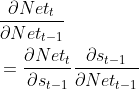    (2.2)

上式出现了一个向量对另一个向量求导，以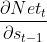为例，Net_t和s_t-1为相同维度向量，不妨设Net_t、s_t-1∈Rⁿ，由①式可看出Net_t中每个元素都是含s_t-1分量的函数：

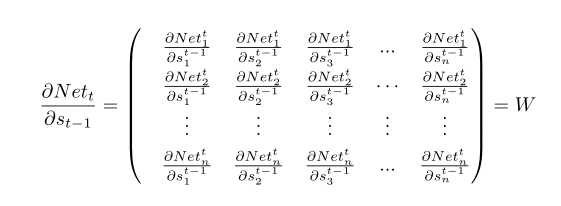
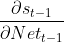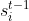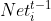类似的，也可求出,由st-1=f(Nett-1)形式可知，st-1任意一个分量仅仅是函数：

综合上面两个公式，在已知δ_t时，上一时刻误差梯度δ_t-1有：

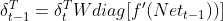   (2.3)

需要注意公式两边都有转置，这是因为W*diag[f'(Nett-1)]是一个n*n的方阵，而δ_t是n行1列的向量，所以δ_t需要先转置后方能运算，这样得到的δ_t-1也是n行1列的向量，假设k是从0到t某一个时刻，从(2.3)式可递归得到k时刻的梯度误差:

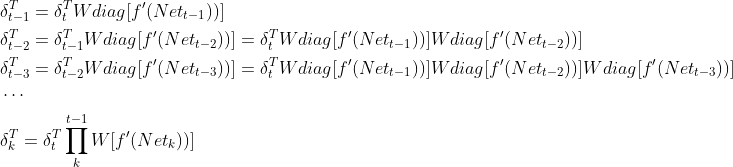
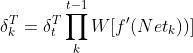     (2.4)

    通过公式2.4即可通过当前时刻的梯度推算出之前任意时刻的误差，接下来再来分析层与层之间的误差传递，RNN的多层结构反向推导与全连接神经网络一致，假设已知t时刻l层误差为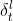,每层之间输入、输出关系为：

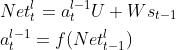
到达l层之前皆为全连接神经网络，l-1层为RNN的起始输入端，这里不仅接受输入向量x_t还要接受来自上一次序列的隐藏层输出s_t-1，设a_l-1为l-1层输出，求导可得：

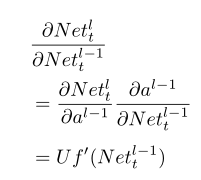
利用上式可得l-1层误差公式：

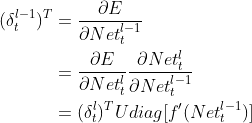    _(2.5)

2.2、求权重参数梯度

通过公式(1.4)、（1.5）可求出任意时刻、任意层的误差梯度，接下来就可以求权重的梯度了，再次列出(1)式:

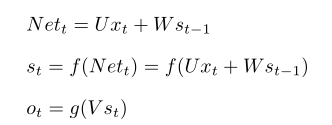
假设输入向量x_t∈R^m,则U∈R^n*m,W∈R^n*n,Net_t、s_t、s_t-1∈Rⁿ,以求矩阵参数W为例:

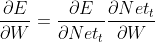    _(2.6)

求W的梯度核心是求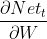，从Net_t定义中可以看出U、x_t与W无关，所以有：

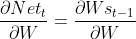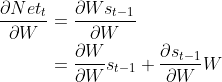
上式代入(2.6)后有：

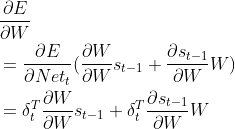   _(2.7)

（2.7）分为两部分，先来看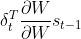，该式中的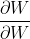是矩阵对矩阵求导，求出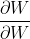后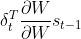将迎刃而解：

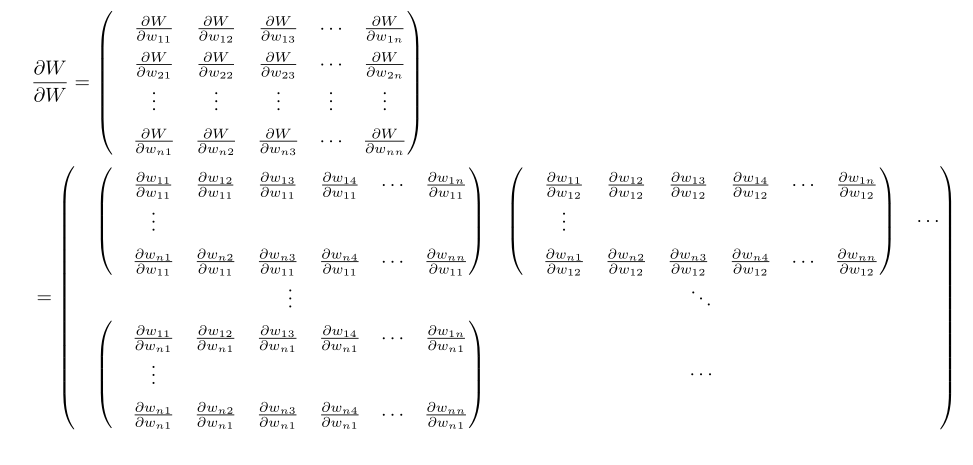
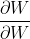是一个克罗内克积（Kronecker积），大小为n²*n²的方阵，由于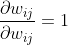所以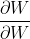是一个少量值为1其余为0的稀疏矩阵，上式可以进一步表示为：