数据在计算机中存储的形式是矩阵，大数据、机器学习、人工智能算法对数据处理，最后都体现为线性代数对矩阵的处理。许多场合中，需要对数据降维以便提取主要特征，本篇介绍利用svd奇异值分解实现这些功能。svd是在机器学习领域有着广泛应用，它不光可以用于降维算法中的特征分解，还可以用于推荐系统、自然语言处理、数据压缩等领域,如Google利用svd分解提取网页特征、形成网页信息索引。

一、常见的矩阵分解

1.1 满秩分解

    矩阵的列代表现实数据的一个属性，数据的某些属性可以用其他属性代替，比如描述一个学生属性有年龄、性别、年级、身高、体重等，一般情况下,知道学生年级,年龄信息就可以推算出来，即年龄可以用年级来代替。矩阵中列可以相互代替，表示为某些列向量是线性相关的，而那些线性不相关的列集合称为矩阵的基，集合中列的数量也称为矩阵的秩，提取矩阵的基后也就提取了数据的主要特征。

   提取矩阵基最常见的是满秩分解，设矩阵A为m行n列矩阵，表达式为A∈R^m*n,秩为r，则存在两个满秩为r的矩阵F∈R^m*r,G∈R^r*n,使得A=FG。简单证明一下：

矩阵A可通过行变换变为一个前r行不全为0，r+1行全为0的行阶梯矩阵，行变换等同于矩阵A左乘行变换矩阵P:

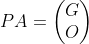
其中G∈R^r*n,为行满秩矩阵，而行变换矩阵P必可逆(可通过行变换将阶梯矩阵再变回A)：

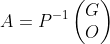
将P^-1按列拆分成(F|S),其中F∈R^m*r为列满秩矩阵:

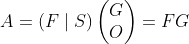    ，证毕！ 

证明的过程同时也是求满秩分解的过程，如有矩阵A:

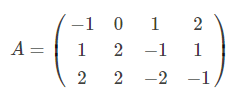
利用高斯消元法行变换后，得到阶梯矩阵:

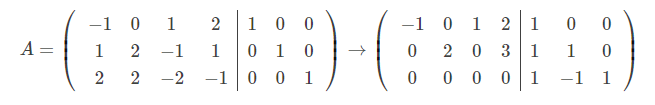
增广矩阵右侧即为行变换矩阵P:

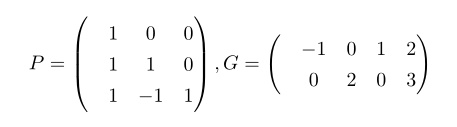
求P逆矩阵：

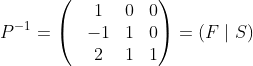
由于r=2,可取矩阵P^-1前2列

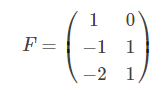
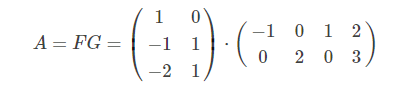
选择矩阵F时不一定选P^-1的前两列，只要任意两个线性不相关列都可以，这里可以看出，满秩矩阵分解是不唯一的。

1.2  QR分解(UR分解)

    设矩阵A∈R^n*n满秩矩阵,则A可以唯一的分解为A=QR。QR分解本质是Gram–Schmidt正交化，当矩阵为复数时，有分解A=UR,此时称为UR分解。R是一个正线上三角矩阵：R对角线对角线以上数据都是正数；Q是一个标准正交矩阵，当矩阵为复数时，U是酉矩阵。标准正交矩阵是酉矩阵的一种，酉矩阵是一个对称矩阵，有以下性质：

U=U^T

UU^T=I。

除了以上性质，酉矩阵每一个列都是单位向量，且任意两个列正交。

可以把满秩方阵A每个列视为一个向量，A=(α₁,α₂,α₃,...α_n),通过施密特正交化得到另一组正交基:β₁,β₂,β₃,...β_n。第一步选α₁作为β₁，将α₂投影到β₁上:

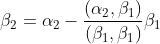
同样可以得到β_3：

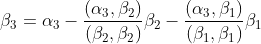
依次类推，可得施密特正交基的通用公式：

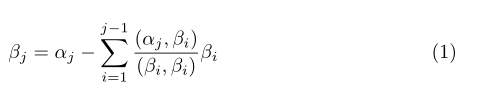
依次将β₁,β₂,β₃,...β_n转为单位向量：

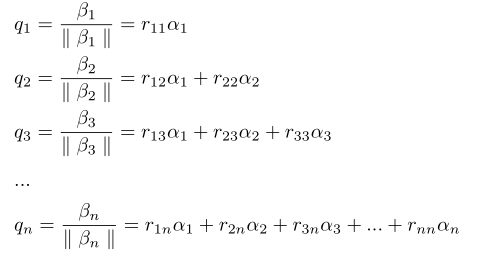
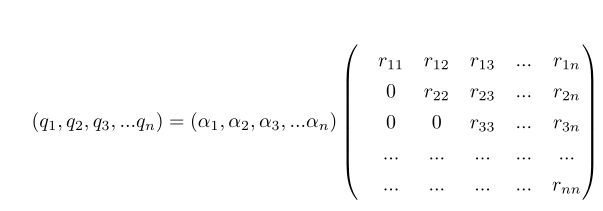
即得到Q=AR,R可逆且逆矩阵仍为正三角矩阵，这样就得到A的QR分解QR^-1=A。

    以上讨论矩阵A是一个满秩的方阵，当矩阵A秩为r的列满秩矩阵时，即A∈R^m*r,rank(A)=r时，有A=QR,其中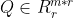，R为正线上三角矩阵;而当A是行满秩矩阵时，即A∈R^r*n,rank(A)=r时,有A=LQ, 其中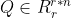,L是一个正线下三角矩阵。如果A是一个常规矩阵，且A∈R^m*n,秩r=rank(A)≦min{m,n}时:

A=Q₁R₁L₂R_2  ②

其中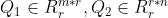,R₁是正线上三角矩阵，L₂是正线下三角矩阵。要证明上式②，可以通过先将A满秩分解，化为两个满秩矩阵后，再将满秩矩阵进行QR分解即可得证。利用公式1，实现QR分解代码如下：

import numpy as np
import  math
import scipy.linalg
#QR分解
def gram_schmidt(A):
    """Gram-schmidt正交化"""
    Q=np.zeros_like(A)
    cnt = 0
    for a in A.T:
        u = np.copy(a)
        for i in range(0, cnt):
            u -= np.dot(np.dot(Q[:, i].T, a), Q[:, i]) # 减去待求向量在以求向量上的投影
        e = u / np.linalg.norm(u)  # 归一化
        Q[:, cnt] = e
        cnt += 1
    R = np.dot(Q.T, A)
    return  Q, R
if __name__=='__main__':
    A = np.array([[6, 5, 9], [5, -1, 6], [5, 1, 4], [0, 4,-4]], dtype=float)
    Q, R=gram_schmidt(A)
    print(A)
    print('='*100)
    print(Q)
    print('=' * 100)
    print(R)

二、SVD分解

    矩阵A是一般矩阵，A∈R^m*n,秩为rank(A)=r，r≦min{m,n},由线性代数知，A^TA是一个n阶方阵，且秩也是r。再引入n个标准正交基向量：v₁,v₂,v₃,....v_n，其中v₁,v₂,v₃,....vr是矩阵A^TA的特征向量，下面线性映射把由v₁,v₂,v₃,....v_n这n个基表示的n维空间映射为另一个n维线性空间：