信息熵、交叉熵、相对熵原理与softmax函数的应用
信息熵在人工智能领域有着举足轻重的作用,在分类的算法中常利用信息熵设计损失函数推导出最优数学模型,softmax函数是一种处理数据手段,一般会出现在模型最后阶段,比如各种神经网络的最后一层,softmax函数可把任意维度数据(一般表现为向量) 处理成概率形式,这样就可以用交叉熵的方法得到与真实概率分布之间损失进而优化模型参数。本篇先介绍信息熵、交叉熵、相对熵,然后对softmax函数做相应介绍。
一、信息熵、交叉熵、相对熵
熵原本是物理中一个热力学概念,熵反应了物质无序的程度,熵越大无序性也越大,任何物质都会自发的向无序状态演变。在计算机信息领域借用了这个概念,用信息熵来反应信息的不确定性,信息熵越大,信息包含的不确定性越大,如果有些信息能够消除不确定性,使熵变小,那么这类信息对我们处理问题就是有益的。比如你老板是一位男性,在电影院陪着家人看电影,你突然有事去找他但不知道具体他在哪个位置,默认情况下要一排一排的找,查找难度代表找人初始的信息熵,如果有人告诉你他在第四排就好找多了,代表着信息熵就变小了,这个第几排的信息对我们消除找人的难度是有帮助的,而如果我告诉的是你老板是一个40岁的男子,这类信息对降低信息熵没丝毫作用,因为你本来就知道这些信息。
1.1 信息熵的概念

1.2 交叉熵与最大似然法
信息熵反映了真实数据的不确定性,这是样本固有的概率特性,人工智能方法需要利用数学模型模拟出一个实验概率分布,让实验概率分布最大程度接近真实概率分布,从侧面了解真实样本的的内在规律,通常利用交叉熵来衡量实验概率与真实概率之间的差距。


利用交叉熵优化分类模型分为两个步骤,先求出实验概率分布与真实分布之间的交叉熵,然后使用交叉熵定义为损失函数并求损失函数最小值;而最大似然法就更为直接,就是求最小的交叉熵,两者殊途同归,核心都是降低交叉熵。
1.3 相对熵
有了信息熵和交叉熵之后就可以定义相对熵的概念了,相对熵=交叉熵-信息熵。严格意义上来说众多"熵"的概念中,相对熵才是真正反映实验概率与真实概率之间差异的“熵”,相对熵越小代表模型与真实概率分布越接近,然而真实数据给定后,信息熵是一个常量,所以常把降低相对熵的转化为降低交叉熵。相对熵是一个大于等于0的数,其值取零时交叉熵等于信息熵,意味着实验概率完全拟合了真实概率。这里会有一个疑问,为什么交叉熵一定大于等于信息熵呢?

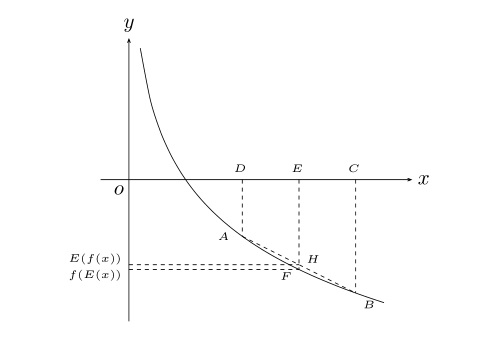


以上一系列推导,可以发现交叉熵是一个构造出来的函数,其性质非常优美,交叉熵将概率知识与分析学完美的结合在一起,机器学习中常用交叉熵来建立损失函数提高模型的准确率。接下来介绍softmax的函数其实并没有太大的创新,只是将数据处理成交叉熵能够接受的形式。通过之前介绍,熵接受的参数是概率,而概率值是[0,1]之间实数,实践当中softmax把各种各样的输入数据都处理成概率形式,再利用这些概率数值生成交叉熵形式的损失函数。
| 上一篇 基变换、线性变换与pca主成分分析 | 下一篇 决策树(上)-ID3与C4.5 |
| 评论区 | |