LSTM-循环神经网络(下)
上篇介绍了RNN循环神经网络,上篇在最后说明了RNN有梯度爆炸和梯度消失的问题,也就是说RNN无法处理长时间依赖性问题,本篇介绍的LSTM(长短时记忆网络)是应用最多的循环神经网络,当提到循环神经网络时一般都特指LSTM,如果以将RNN视为一种思想,那么LSTM是循环神经网络的具体实现。通过‘门’运算引入细胞状态的概念(Cell state),LSTM可以较好的利用历史记录信息。
一、lstm前向传播
lstm的模型类似于数字电路,lstm按时间维度展开后模型如下图所示:
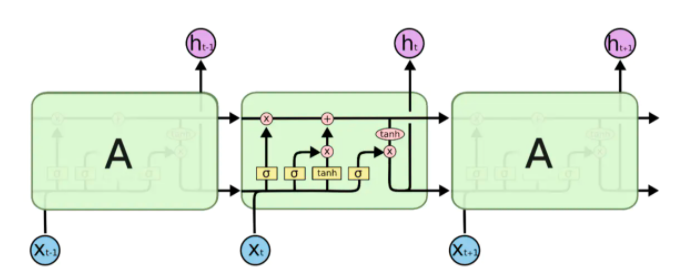
lstm比起其他类型神经网络多出了一个‘门’的概念,在数字电路中通过'与门'、‘或门’、‘异或门’等有机结合可以组成具有复杂功能的电路,lstm借鉴了这种思想,只不过是通过软件实现这些门电路,在刘慈欣的小说《三体》中,牛顿和冯.诺依曼利用3000千万士兵组成一台有CPU、内存、硬盘的人肉电脑,这与lstm的设计思想其实有异曲同工之妙。
lstm中有满足不同需求的'与门',在神经网络中'与门'是一个值在0到1之间向量,门向量与具体信息一般是以按位相乘的方式运算(哈达玛积),当门向量元素值为0时代表抑制该位置的信息,而向量元素值为1时代表让该位置的信息通过,首先看下lstm中的遗忘门,我们用符号ft表示:
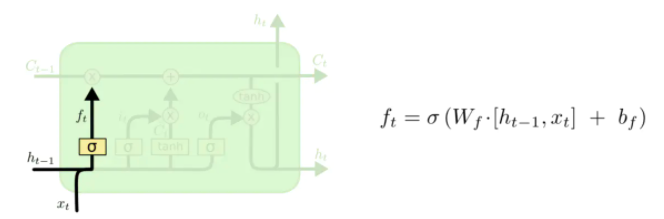
上图中σ代表sigmod函数,ht-1是上一个序列的输出,xt为本次输入,可以看出遗忘门其实一个简单全连接神经网络,该神经网络是训练出各种具有过滤功能'门',与此类似还有'输入门'it、'候选门'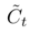 :
:
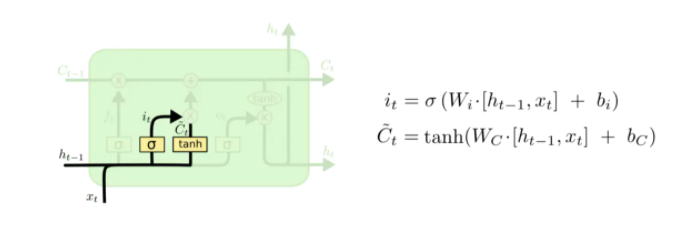
有了这几个门之后就可以引入LTSM的核心:细胞状态Ct
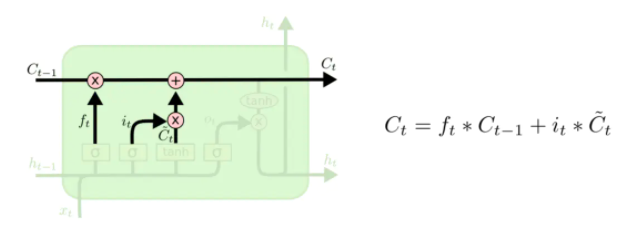
每个时刻的细胞状态Ct分为两个部分,其中一部分有取舍的选择了上一次细胞状态值Ct-1,另外一部分来自本次的输入,更新完Ct后即可通过输出门ot得到此时的输出ht:
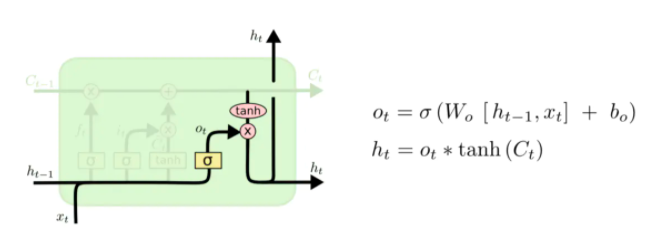
由于引入了数字电路模型形式,lstm的模型比起之前介绍神经网络稍微复杂些。lstm原理类似于中国古代的‘万年历’,‘万年历’是古代人记录的自然界规律信息,这与lstm需要解决的时间序列问题很相似,有了'万年历’后,根据最近已发生的现象即可按图索骥定位到'万年历’对应的部分,这样就可根据'万年历’预测接下来的走势。再引用一下《三体》小说里情节,小说中三体世界里的墨子总结出一套'万年历’,他通过长期观察并记录三个太阳的运动轨迹数据,结合已经发生事件即可预测'恒纪元'与'乱纪元'更迭。
有了以上类比后再来看lstm前向传播过程,输出ht代表了一个需要预测信息,而ht由输出门和Ct运算得到,Ct公式:
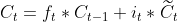
Ct其中包含历史信息的Ct-1和本次输入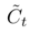 ,这与查找定位'万年历’过程是一致的:通过Ct-1和
,这与查找定位'万年历’过程是一致的:通过Ct-1和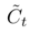 定位到'万年历’相应的部分即可得到预测数据ht,输出门ot的作用是提取细胞状态主要信息后输出,ot增强了模型的非线性拟合能力。
定位到'万年历’相应的部分即可得到预测数据ht,输出门ot的作用是提取细胞状态主要信息后输出,ot增强了模型的非线性拟合能力。
再来看细胞状态Ct,Ct含上一次信息Ct-1,与此类似Ct-1含Ct-2的信息,递归的存在导致Ct的输入中含有0到t-1时刻的全部的细胞状态信息,这些累积的信息不一定对此时t时刻预测都有用处,对Ct-1信息应有适当的取舍,如同做英语完形填空时,通过语义、语境的分析后,空缺处单词与段落中几个单词有关系,而与另外语句、单词没有任何关系,lstm对信息的取舍是通过遗忘门ft来实现的,前面说过,包括遗忘门在内所有门本质是全连接神经网络,以遗忘门为例:
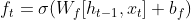
ht-1含有历史的输出信息,ht-1与xt合并为一个向量作为ft输入,可以理解ht-1与xt组成了一个t时刻上下文,类似于完形填空中空缺处的上下文语境,通过全连接神经网络训练后,ft知道如何选择性的利用上下文信息推导出预测值ht,输入门it的作用也一样,通过训练后,可以选择性提取输入信息的主要特征推导出预测值ht,输入门与输出门互相配合后更新细胞状态Ct。
以一个例子说明lstm的运行过程,下面代码利用lstm拟合函数y=3sinx+5cos5x+6
import numpy as np
import math
import torch
from torch import nn, optim
import matplotlib.pyplot as plt
modelname = 'model/lstmfunction'
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
datainterval=10
def load(num):
x=range(num)
#y=3sinx+5cos5x+6
y=[float(3*math.sin(t)+ math.cos(5*t)+np.random.randn(1,1)+6) for t in x]#每个数据加上一个标准正态随机波动
return np.array(y,dtype=np.float32)
class lstm(nn.Module):
def __init__(self, input_size , hidden_size , output_size , num_layer,bidirect =1,dropout=0.1 ):
super(lstm, self).__init__()
self.hiddensize= hidden_size
self.bidirectional=bidirect
self.layer1 = nn.LSTM(input_size, hidden_size, num_layer ,bidirectional=False if bidirect==1 else True )
self.Dropped = nn.Dropout(dropout)
self.Tanh = nn.Tanh()
self.layer2 = nn.Linear(hidden_size*bidirect, output_size)
self.BN=nn.BatchNorm1d(datainterval)
def forward(self, x):
#Batch Normalize:归一化处理:防止梯度爆炸或消失
input=self.BN(x)
#转换成batch*seqlen*inputsize格式
input = input.view(-1, datainterval, 1)
# 转换成seqlen*batch*inputsize格式
x = torch.transpose(input, 0, 1)
out,(hidden,_) = self.layer1(x)
#取每个序列的最后一个输出
out = out[-1, :, :]
out=out.view(-1, self.hiddensize*self.bidirectional)
out= self.Dropped (out)
out = self.layer2(out)
return out
def create_dataset(num,trainfactor, interval ):
dataset = load(num)
dataX, dataY = [], []
for i in range(len(dataset) - interval):
a = dataset[i:(i + interval)]
dataX.append(a)
dataY.append(dataset[i + interval])
X,Y=np.array(dataX), np.array(dataY)
train_size = int( X.shape[0] * trainfactor)
train_X, train_Y, test_X, test_Y = X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]
train_X = train_X.reshape(-1, datainterval )
train_Y = train_Y.reshape(-1, 1 )
test_X = test_X.reshape(-1, datainterval )
test_Y = test_Y.reshape(-1, 1 )
train_x =torch.from_numpy(train_X)
train_y = torch.from_numpy(train_Y)
test_x = torch.from_numpy(test_X)
test_y = torch.from_numpy(test_Y)
return train_x, train_y, test_x, test_y
def train(train_x, train_y):
model = lstm(1, 200, 1, 2)
model.train()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)
iternum=5000
for e in range(iternum):
# 前向传播
out = model(train_x)
loss = criterion(out, train_y)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (e + 1) % 1000 == 0:
torch.save(model, modelname )
if (e + 1) % 1000 == 0: # 每 100 次输出结果
print('迭代数: {}, 损失值: {:.6f}'.format(e + 1, loss.data.item()/train_x.shape[0]) )
print('\r')
def test(num,trainfactor=0.8):
model = torch.load(modelname)
model.eval()
dataset = load(num)
train_size = int(dataset.__len__() * trainfactor)
dataset=dataset[train_size:]
startnum=datainterval
predictnum = 50
x=range(startnum,startnum+predictnum)
y=dataset[startnum:startnum+predictnum]
y_=[]
#取得初始10个数据来预测接下来50个样本点
data=[x for x in dataset[:datainterval]]
for i in range(0,predictnum):
seed = np.array(data[i:i+datainterval],dtype=np.float32)
seed=seed.reshape(-1, datainterval )
p=model(torch.from_numpy(seed))
y_.append(p.item())
data.append(p.item())
plt.plot(x, y, color='blue')
plt.plot(x, y_, color='red')
plt.grid()
plt.show()
if __name__=='__main__':
runtest = True
if (runtest):
test(2000)
else:
train_X, train_Y, test_X, test_Y = create_dataset(500, 0.8, datainterval)
train(train_X, train_Y)利用test函数测试模型效果如下:
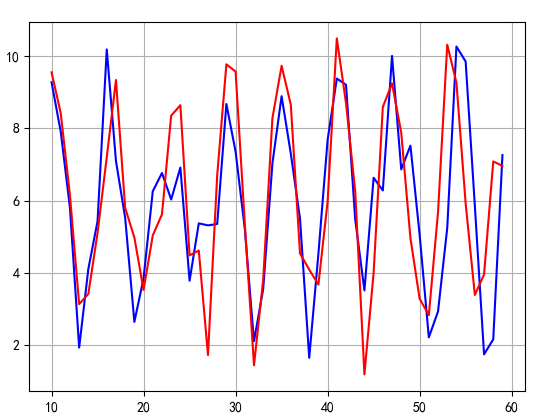
蓝色线是目标函数走势,红色线是lstm的预测走势图,模型基本上模拟出了实际数据走势,如果利用GPU并增加迭代次数模型效果会更好一些。
二、lstm反向传播推导
首先列出lstm前向传播中公式组,包含四个门以及两个输出:
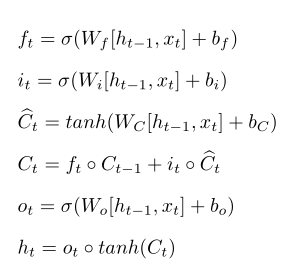 (1)
(1)
为推导方便,对带激活函数的公式定义其输入部分,如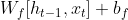 定义为遗忘门ft在t时刻输入:
定义为遗忘门ft在t时刻输入:
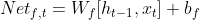
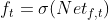
可将权重矩阵Wf拆解为Wfh、Wfx两个矩阵,Wfh、Wfx分别与ht-1和xt相乘:
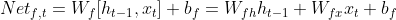
类似的,可以定义以下的输入公式组:
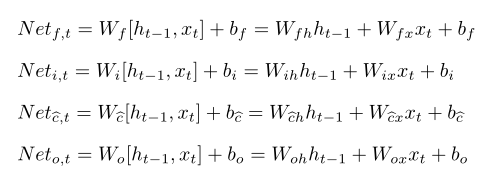 (2)
(2)
假设已知t时刻误差δt,由于lstm的输出ht没有使用激活函数,δt定义为:
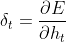
根据链式求导法则,已知δt后上一时刻误差δt-1为:
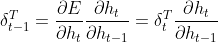 (3)
(3)
求δt-1核心是求出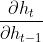 ,比起RNN,lstm求解这一层次梯度稍微复杂些,观察(1)公式组,ht等式右侧ot和Ct都含有ht-1,而Ct中ft、it、
,比起RNN,lstm求解这一层次梯度稍微复杂些,观察(1)公式组,ht等式右侧ot和Ct都含有ht-1,而Ct中ft、it、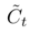 都含有ht-1,逐项使用链式求导法则得:
都含有ht-1,逐项使用链式求导法则得:
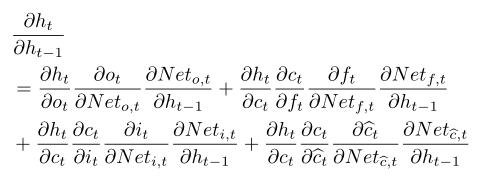
| 上一篇 RNN-循环神经网络(上) | 下一篇 seq2seq、Attention注意力机制 |
| 评论区 | |