NMF非负矩阵分解是将一个非负矩阵分解成两个非负矩阵，处理有些实际问题时数据往往是非负数，其他的矩阵分解如SVD分解有时会将矩阵分解成含有负数矩阵，负数出现与实际情况相悖。NMF在图像处理、推荐系统、数据降维中有着广泛的应用，NMF在实现方法上也与其他矩阵分解有质的区别。

一、理解NMF

   NMF将一个非负矩阵V分解成两个非负矩阵W、V，三者的关系是：

V≈W*H

注意中间是约等于的关系，NMF需要找出两个非负矩阵来近似原来的矩阵。不妨设V是m行n列的矩阵：V∈R^m*n,W是m行r列矩阵：W∈R^m*r,H是r行n列矩阵：H∈R^r*n。从几何角度看，V代表了一个n维线性空间，W代表了一个r维线性空间，由于r<n,所以W是V的子空间，H矩阵代表系数矩阵，也可以理解为坐标矩阵，所以也可以这样定义NMF：找到一个线性空间V的子空间W，使得空间V中的向量投影到子空间W中后误差最小，如下图：

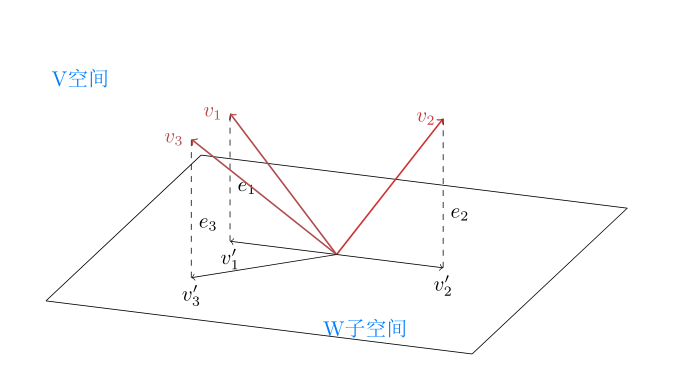
v₁,v₂,v₃是V空间的向量，e₁,e₂,e₃是v₁,v₂,v₃投影到W子空间后的误差，满足所有误差最小子空间W即为目标矩阵，在NMF算法中W称为基矩阵，H称为系数矩阵。

    来看一个具体的例子，下面的程序根据10位受访者对10部影片打分，利用NMF可分别对用户和电影进行分类：

import numpy as np
from sklearn.decomposition import NMF
from _collections import defaultdict
import  matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
if __name__=='__main__':
    ratings = [
        [5.0, 5.0, 4.5, 4.5, 5.0, 3.0, 2.0, 2.0, 0.0, 0.0],
        [4.2, 4.7, 5.0, 3.7, 3.5, 0.0, 2.7, 2.0, 1.9, 0.0],
        [2.5, 0.0, 3.3, 3.4, 2.2, 4.6, 4.0, 4.7, 4.2, 3.6],
        [3.8, 4.1, 4.6, 4.5, 4.7, 2.2, 3.5, 3.0, 2.2, 0.0],
        [2.1, 2.6, 0.0, 2.1, 0.0, 3.8, 4.8, 4.1, 4.3, 4.7],
        [4.7, 4.5, 0.0, 4.4, 4.1, 3.5, 3.1, 3.4, 3.1, 2.5],
        [2.8, 2.4, 2.1, 3.3, 3.4, 3.8, 4.4, 4.9, 4.0, 4.3],
        [4.5, 4.7, 4.7, 4.5, 4.9, 0.0, 2.9, 2.9, 2.5, 2.1],
        [0.0, 3.3, 2.9, 3.6, 3.1, 4.0, 4.2, 0.0, 4.5, 4.6],
        [4.1, 3.6, 3.7, 4.6, 4.0, 2.6, 1.9, 3.0, 3.6, 0.0],
    ]
    movie={
        1:'星球大战',
        2:'黑客帝国',
        3:'盗梦空间',
        4:'哈利波特',
        5:'霍比特人',
        6:'六壮士',
        7:'拯救大兵瑞恩',
        8: '兵临城下',
        9: '魔窟寻谍',
        10: '大逃亡'
    }
    A=np.asmatrix(ratings,dtype=np.float)
    max_components=2
    nmf=NMF(n_components=max_components, init='random', random_state=1)
    A_dash=nmf.fit_transform(A)
    F=nmf.components_
    xf,yf=F[0,:],F[1,:]
    for i in range(A_dash.shape[0]):
        print('用户id:%d 成分1得分:%0.2f 成分1得分:%0.2f'%(i+1,A_dash[i,0],A_dash[i,1]))
        print()
    print('='*50)
    for i in range(F.shape[1]):
        print('%s 成分1得分:%0.2f 成分1得分:%0.2f'%(movie[i+1],F[0,i] ,F[1,i] ))
        print()
    plt.figure(1)
    plt.title('基矩阵')
    x,y=A_dash[:,0],A_dash[:,1]
    plt.scatter(x,y)
    plt.xlabel('成分1得分')
    plt.ylabel('成分2得分')
    for i in range(A_dash.shape[0]):
        plt.annotate(i+1, (A_dash[i, 0], A_dash[i, 1]) )
    plt.figure(2)
    plt.title('系数矩阵')
    plt.scatter(xf, yf)
    plt.xlabel('成分1得分')
    plt.ylabel('成分2得分')
    for i in range(F.shape[1]):
        plt.annotate(movie[i+1],(F[0,i] ,F[1,i] ))
    plt.show()

ratings变量代表受访者的打分信息，是一个10*10的非负矩阵，上述代码利用nmf将ratings分解成两个矩阵，一个是矩阵A_dash∈R^10*2,A_dash对应NMF分解的基矩阵，打印A_dash有以下信息：

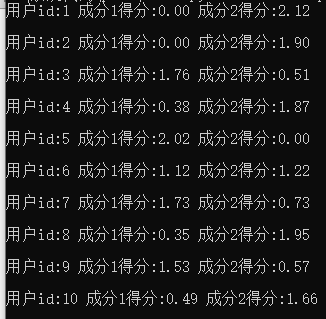
根据A_dash可以对用户进行分类，比如id=1的用户，根据打分的情况可以判断出他偏好成分2的电影，但不喜欢成分1的电影，再比如id=3的用户偏好成分1的电影，而成分1和成分2分别对应哪些题材电影呢？这可以通过系数矩阵收集到相应信息，系数矩阵对应代码中矩阵F，打印F矩阵信息如下：

可以看出星球大战成分2得分较多，id1和id2的用户都喜欢星球大战、黑客帝国、霍比特人这类电影，这当然不是偶然的，可以发现成分2得分较多的电影大都是科幻、魔幻类电影，而成分1得分较多的是战争题材电影。这样一来就通过NMF对受访者以及电影实现了分类，如下图：

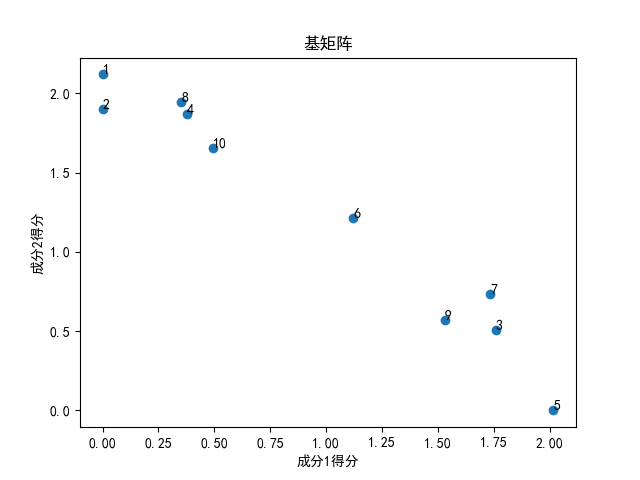
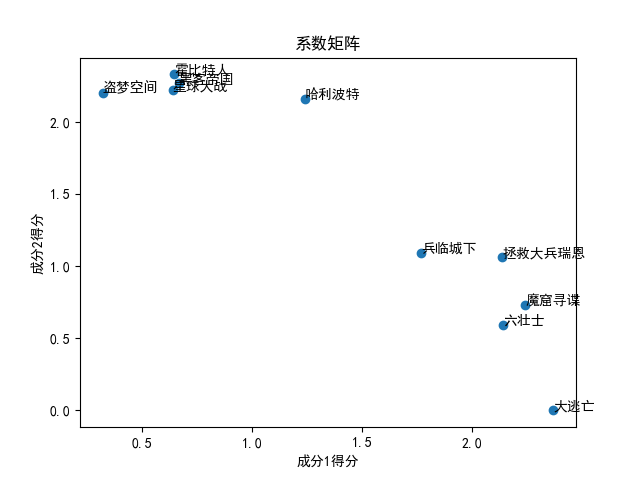
还可以利用NMF开发推荐系统，比如一个用户没有对其中一个偏好成分1（战争题材电影）的电影打分，但通过用户对其他电影打分可以判断出该用户偏向于成分1的电影，那么就可以向其推荐战争题材的电影。

二、NMF公式推导

2.1、矩阵范数

    在分析向量、矩阵时，常常利用范数将向量、矩阵变为一个实数，变为实数后就可以利用多种手段如微分、积分、幂级数等手段做进一步处理。设有一个矩阵A∈R^m*n,矩阵A的任意一个元素用a_ij表示，常用矩阵范数形式有1-范数：

Frobenius范数或称F-范数:

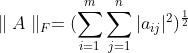
范数几何意义是向量或矩阵的长度，当线性空间引入范数后也就有了距离的概念，这很好理解，比如两个向量v和u,v-u代表两者之间一个向量，而范数||v-u||就表示v和u之间向量长度，也就得到了v和u之间距离，所以线性赋范空间是一个距离空间。距离空间与熟识欧几里得空间还差一个角度的概念，角度需要在距离空间的基础上再引入内积。

    基矩阵W与系数矩阵H相乘后的矩阵用B表示，V-B表示分解后矩阵B与原矩阵V的误差，结合上面的分析，范数||V-B||较小时说明B与原矩阵有较好的相似性，NMF算法的目标可以描述为求下面F-范数平方的最小值：

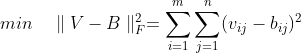              ①

设W是m行r列矩阵：W∈R^m*r,H是r行n列矩阵：H∈R^r*n，则b_ij可表示为：

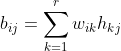                                            ②

②代入①式后可得下面的损失函数：

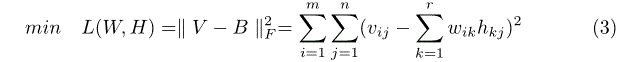
公式(3)中共有m*n个未知参数，可以通过梯度下降法求未知参数，上式中由于含有平方项，为后期处理方便通常把损失函数表示成下面的形式：

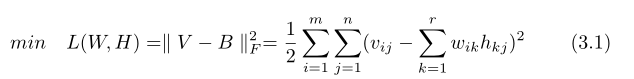
2.2 、最大似然法推导损失函数

    上面利用范数导出导出了损失函数(3.1)式，接下来利用最大似然法从另一个角度理解NMF算法，依然利用之前的假设：基矩阵W与系数矩阵H相乘后的矩阵用B表示，则V=B+E,E代表了V与B之间的误差，具体到矩阵每个元素可以这样表示：

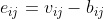
假设e_ij为数学期望为0，方差为σ²的正态分布，即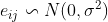，最大似然法即为求下面函数最大值：

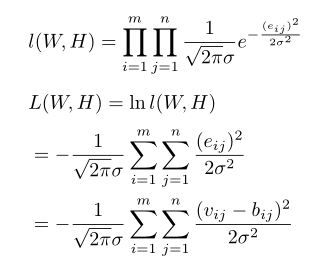
由于方差σ大于0，所以求上式最大值实质为求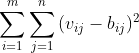最小值，这与用矩阵范数导出的损失函数是一致的，这个结论并不是偶然的，矩阵法本质是最小二乘法，而最小二乘法、线性回归都是将误差设定为正态分布。NMF在应用中根据实际情况，误差项也可以用其他概率分布实现，之前文章曾介绍过，最大似然法与求交叉熵最小值是本质一个问题，如果将泊松分布与熵模型结合可以得到NMF另一种损失函数形式-KL散度损失函数，形式如下：

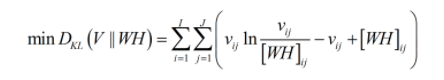
本篇重点研究矩阵分解后误差为正态分布的情况，即NMF损失函数为公式(3.1)，接下来对式(3.1)求导得到各个参数梯度。

2.3、求损失函数最优解

    设w_it为基矩阵W（W∈R^m*r，t≤r）任意一个元素，由链式法则有：

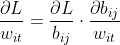
由公式②可得:

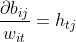
而当确定w的下标i和t后，观察可以发现：w_it只与矩阵B=W*H的第i行向量有关，所以有:

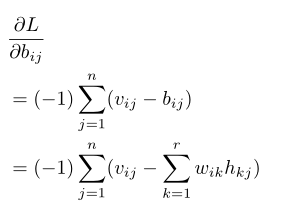
这样得到未知参数w_it的梯度为：

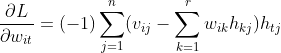    ④

注意，④式中i和t是常量，j,k是迭代变量，通常④式写成下面矩阵相乘的形式：

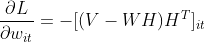        (4.1)

同理，可以得到系数矩阵H任意一个元素h_tj的梯度：

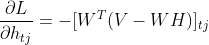       (4.2)

求目标函数最小值，则需要按梯度反方向更新参数：

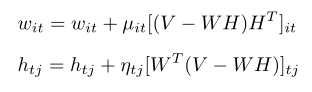
上式中μ_{it 、} η_tj称为步长系数，在神经网络中也成为学习率，可以发现NMF算法中每个未知参数的步长系数都是不同的，最重要的一点，NMF必须确保分解后矩阵是非负数，μ_it 、 η_tj取数是受到一定限制的，可以通过下面的换元法保证分解后矩阵的非负性：

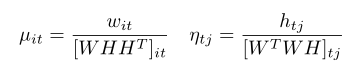
可得到未知参数最终的迭代计算公式：

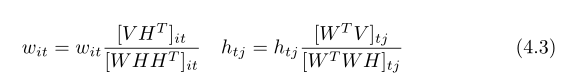
通过换元法变换步长系数不仅能确保矩阵分解后非负，还能简化计算变为矩阵乘法。

三、NMF代码实现

    利用以上推导过程实现NMF，示例代码通过公式(4.3)求出(3.1)最优解后得到未知参数，并将分解后矩阵与sklearn自带的NMF算法比较，通过矩阵范数计算可以发现两者准确率是相同的。