马尔科夫链是离散的马尔科夫过程，而马尔科夫过程是一类平稳的随机过程。如果一个时间序列是马尔科夫链，设时间序列在每个时刻的状态有n种状态S={s₁,s₂,s₃,..s_n},在m时刻为s_i,则在m+k时刻的状态s_j只与m时刻相关，与m-1,m-2,m-3...,1时刻无关:

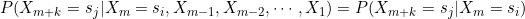
上面的条件概率说明了马尔科夫链未来状态(m+k)仅与当前状态有关(时刻m)有关，而平稳过程表明时间序列状态的转移与起始点m也无关，仅与k有关，关于平稳随机过程的定义请参见时间序列分析:AR(p),MA(q)，满足平稳性的马尔科夫过程也称齐次马尔科夫过程。常研究马尔科夫链k=1时各个状态转移情况，用a_ij表示从状态s_i到下一时刻状态为s_j的概率，如果隐藏变量有n种状态，则马尔科夫链的状态转移矩阵大小是。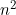

隐马尔科夫链HMM是含有隐变量马尔科夫过程，关于隐变量在EM算法中曾提过。举一个例子，有三个箱子分别标记为1号箱、2号箱、3号箱，每个箱子各有一定比例的白色球和红色球，现将箱子标记遮住，每次随机选择一个箱子、抽取一个球，得的的一组按次序摆放的白、红球称为观察变量，每次选择的箱子是隐藏变量，隐马尔科夫链暗含了两个随机过程，一个是选择箱子的序列，另一个是观察球序列，箱子之间状态的转移称为转移概率矩阵(A)，每个箱子含有白色球、红色球的比例称为发射矩阵(B)，另外，初始时选择各个箱子的概率称为初始概率向量（Pi），三个变量构成一个参数集合可用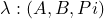表示。HMM常见的有三类问题，分别是：

1、评估问题：已知λ，求出现某种观察结果的概率。

2、解码问题：已知λ，通过观察结果求出隐藏状态序列。

3、学习问题：λ未知，通过观察结果求解λ。

一、评估问题

1.1 前向算法、后向算法

可以用穷举法计算观察结果的概率P(O|λ)，但当观察结果序列很长时穷举法的复杂度很高，前向、后向算法是利用递归方式实现评估问题求解，可大大降低算法运算量，前向算法中首先引入前向概率：

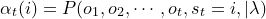  (1.1)

前向概率是联合概率，表示当前面t个观察结果已知时，在t时刻隐藏状态为i观察结果为o_t的概率，利用加法原理可知在t+1时刻的前向概率为：

    (1.2)

(1.2)中n为隐藏状态的数量，a_ji是转移概率矩阵中相对应的元素，b_i(o_t+1)是发射概率矩阵中相对应的元素，如果观察结果的长度为T，很容易得到观察结果概率P(O|λ)：

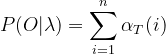       (1.3)

前向算法的初值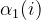需要利用初始概率矩阵：

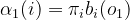
与前向算法相反的是后向算法，后向算法中后向概率的定义为：

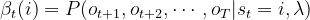   (1.4)

后向概率从观察结果后端向前计算，另外观察(1.4)可知后向概率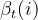并不知道时刻t的观察结果o_t，此时只有t+1,t+2,..T时刻的观察结果是已知的，根据(1.4)可得到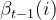形式：

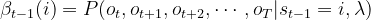
假设t-1时刻隐藏状态为s_i、t 时刻隐藏状态为s_j,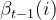可以看成由两个部分组成，第一部分是出现观察结果o_t的概率，即为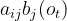：,另一个是t时刻隐藏状态为sj、观察结果o_t+1，o_t+2，o_t+3，o_T的概率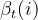：，利用乘法定理可知，此时的概率为：

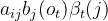
而t时刻隐藏状态可能性有n个，利用加法原理可得：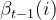

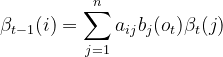  (1.5)

由上面推导可递归得到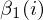

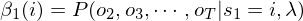
在t=1时刻，从隐藏状态s_i得到o₁的概率为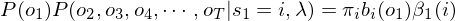,由加法原理可知后向算法P(O|λ)为：

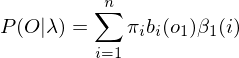  (1.6)

后向概率的初始概率为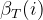，可以表示为：

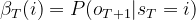
实际上o_T+1是观察不到的，可以认为在T时刻隐藏状态每种可能性都有，可设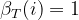，利用上面公式来实现开篇箱子抽取红白球的评估问题：

from hmmlearn import hmm
import numpy as np
#隐变量，3个箱子
states = ['box1', 'box2', 'box3']
#观察结果状态：红色球、白色球
observations = ["red", "white"]
n_states = len(states)
start_probability = np.array([0.2, 0.5, 0.3],np.float64)

transition_probability = np.array([
    [0.5, 0.2, 0.3],
    [0.3, 0.5, 0.2],
    [0.2, 0.3, 0.5]
],np.float64)

emission_probability = np.array([
    [0.5, 0.5],
    [0.4, 0.6],
    [0.7, 0.3]
],np.float64)
class HMM(object):
  def __init__(self, A, B, pi):
    '''''
    A: 状态转移概率矩阵
    B: 输出观察概率矩阵
    pi: 初始化状态向量
    '''
    self.A = np.array(A)
    self.B = np.array(B)
    self.pi = np.array(pi)
    self.N = self.A.shape[0]  # 总共状态个数
    self.M = self.B.shape[1]  # 总共观察值个数

  # 前向算法
  def forward(self,   O ):
    '''''
    T: 观察序列的长度
    O: 观察序列
    alpha: 前向概率数组
    '''
    T=len(O)
    alpha = np.zeros((T, self.N), np.float64)
    # 初始化
    for i in range(self.N):
      alpha[0, i] = self.pi[i] * self.B[i, O[0]]

    # 递归
    for t in range(T-1):
      for j in range(self.N):
        sum = 0.0
        for i in range(self.N):
          sum += alpha[t, i] * self.A[i, j]
        alpha[t+1, j] = sum * self.B[j, O[t+1]]

    # 终止 公式(1.3)
    sum = 0.0
    for i in range(self.N):
      sum += alpha[T-1, i]
    return sum

  def back(self, O):
    '''''
    T: 观察序列的长度  len(O)
    O: 观察序列
    beta: 后向概率数组
    '''
    T=len(O)
    beta = np.zeros((T, self.N), np.float64)
    # 初始化
    for i in range(self.N):
      beta[T-1, i] = 1.0

    # 递归
    for t in range(T-2, -1, -1): # 从T-2开始递减；即T-2, T-3, T-4, ..., 0
      for i in range(self.N):
        sum = 0.0
        for j in range(self.N):
          sum += self.A[i, j] * self.B[j, O[t+1]] * beta[t+1, j]

        beta[t, i] = sum

    # 终止 公式(1.6)
    sum = 0.0
    for i in range(self.N):
      sum += self.pi[i]*self.B[i,O[0]]*beta[0,i]

    return  sum

#评估问题
def assessment():
    obs = [1,1, 0 ,0 ,1,0,1,0,1,0,0]
    model = hmm.MultinomialHMM(n_components=n_states, n_iter=100, tol=1e-3)
    model.startprob_ = start_probability
    model.transmat_ = transition_probability
    model.emissionprob_ = emission_probability
    score = model.score(np.array([obs]).T)
    #利用hmm库计算观察结果概率
    print("MultinomialHMM P(O|λ):%f" % (np.exp(score)))
    _hmm = HMM(transition_probability, emission_probability, start_probability)
    print("前向概率 P(O|λ):%f"%(_hmm.forward( obs ))  )
    print("后向概率 P(O|λ):%f" % (_hmm.back( obs )))

if __name__ == '__main__':
    assessment()

1.2  单个状态概率,两个状态概率

由前向概率和后向概率可得到另外两个有用的概率:单个状态概率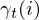,两个状态概率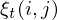，这两个概率都是条件概率，表示固定一个或两个时刻，计算特定隐藏状态转至观察结果的概率，在后面的'学习问题'中将要使用这两个概率。单个状态概率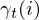定义为：

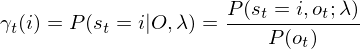 (1.7)

上式分子的联合分布概率表示在t时刻，隐藏状态为i而观察结果为o_t的概率。o_t出现在整个观察结果的中间部分，整个观察结果在时刻t可划分为两部分：o₁，o₂，o₃，...，o_t;o_t+1，o_t+2，o_t+1，...,o_T。前半段可用前向概率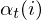表示，后半段可用后向概率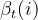表示，利用乘法原理可知联合概率分布为：

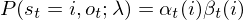   (1.7.1)

分母P(o_t)表示t时刻观察结果为o_t的概率，由加法原理知：

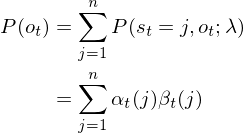(1.7.2)

（1.7.1），（1.7.2）代入（1.7）中可得单个状态概率：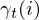

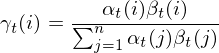     (1.8)

两个时刻状态概率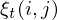定义为在时刻t隐藏变量状态为i,t+1时刻隐藏变量为j:

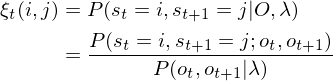(1.9)

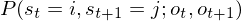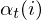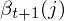可利用前后概率计算出联合概率，此时观察结果仍可视为两个部分：o₁，o₂，o₃，...，o_t;o_t+1，o_t+2，o_t+1，...,o_T。前半段用表示，而可表示为：

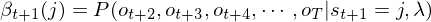
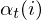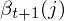，表示观察结果序列少了在t+1时刻观察值o_t+1的概率，而在t+1时刻隐藏变量值是j,所以o_t+1的概率为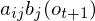,由乘法原理知联合概率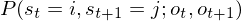结果为：

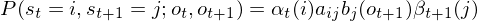   (1.9.1)

(1.9.1)并结合加法原理可得分母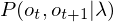公式形式：

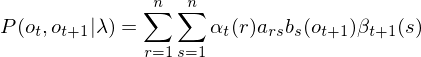        (1.9.2)

(1.9.1)、(1.9.2)代入公式(1.9)得两时刻概率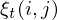公式为：

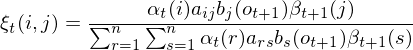   (1.10)

二、解码问题

2.1 维特比算法

解码问题是在已知参数集合λ(A,B,Pi)前提下，通过观察结果得到隐藏变量的序列，如开篇介绍的抽取小球问题中，通过红白球的结果得到每次选择的箱子编号。解码问题可用穷举法实现，实际应用使用基于动态规划的维特比算法，关于动态规划知识点请参见动态规划解决背包问题。如有一个隐马尔科夫链隐藏状态为3个，并得到含有3个数值的观察结果，如下图所示：

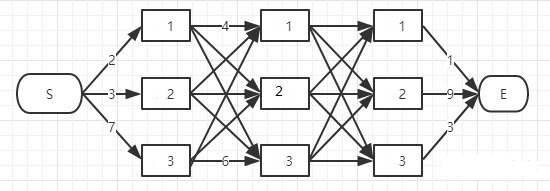
在t=1时刻称为第1阶段，分别列出3个隐藏状态转为观察结果o₁概率：

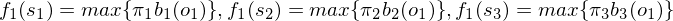
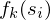称为指标函数值，k表示处在动态规划的哪个阶段，si表示在该阶段结束时的状态，同样的可以列出在第2阶段指标函数：

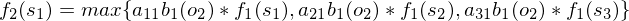
f₂(s₁)的函数中有三项，代表着从阶段1到阶段2状态为s1时有三种可能，如下图所示：

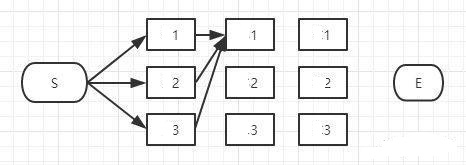
根据最大似然法,利用max函数将三种可能性最大值作为指标函数f₂(s₁)的值，按此规律可以得到f₂(s₂)、f₂(s₃)：

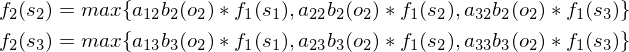
从S端到状态1或状态2、3称为一个决策，由于f₁(s₂)、f₁(s₂)、f₁(s₃)都是已知值，所以f₂(s₂)、f₂(s₂)、f₂(s₃)也可以求出具体数值，可列出第3阶段各个指标函数：

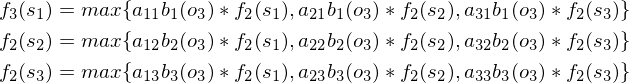
到E代表动态规划终止，此时有：

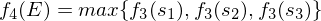
f₄(E)为观察结果的最大概率，从E点逆向追溯到开始状态S，取各个阶段指标函数的最大值所对应的状态就可得到解码问题的解，同时也是隐藏状态最优解，维特比算法是逆向推导的动态规划，下面代码实现了维特比算法：

from hmmlearn import hmm
import numpy as np
#隐变量，3个箱子
states = ['box1', 'box2', 'box3']
#观察结果状态：红色球、白色球
observations = ["red", "white"]
n_states = len(states)
start_probability = np.array([0.2, 0.5, 0.3],np.float64)

transition_probability = np.array([
    [0.5, 0.2, 0.3],
    [0.3, 0.5, 0.2],
    [0.2, 0.3, 0.5]
],np.float64)

emission_probability = np.array([
    [0.5, 0.5],
    [0.4, 0.6],
    [0.7, 0.3]
],np.float64)
class HMM(object):
  def __init__(self, A, B, pi):
    '''''
    A: 状态转移概率矩阵
    B: 输出观察概率矩阵
    pi: 初始化状态向量
    '''
    self.A = np.array(A)
    self.B = np.array(B)
    self.pi = np.array(pi)
    self.N = self.A.shape[0]  # 总共状态个数
    self.M = self.B.shape[1]  # 总共观察值个数

  #维特比算法
  def viterbi(self, O):
      self.O = O
      T = len(self.O)
      I = np.zeros(T,  int)
      #f是每个阶段的指标函数
      f = np.zeros((T, self.N), np.float64)
      #strategies 保存指标函数中max{...}最大值项对应的状态，方便在追溯时得到隐藏状态序列
      strategies = np.zeros((T, self.N), np.float64) 
      for i in range(self.N):
          f[0, i] = self.pi[i] * self.B[i, self.O[0]]
          strategies[0, i] = 0

      for t in range(1, T):
          for i in range(self.N):
              #计算指标函数
              f[t, i] = self.B[i, self.O[t]] * np.array([f[t - 1, j] * self.A[j, i]
                                                             for j in range(self.N)]).max()
              #得到max{...}最大值项对应的状态
              strategies[t, i] = np.array([f[t - 1, j] * self.A[j, i] for j in range(self.N)]).argmax()

      I[T - 1] = f[T - 1, :].argmax()
      # 逆向回溯
      for t in range(T - 2, -1, -1):
          I[t] = strategies [t + 1, I[t + 1]]
      return I

#解码问题
def decode():
    obs = [1,1, 0 ,0 ,1,0,1,0,1,0,0]
    model = hmm.MultinomialHMM(n_components=n_states, n_iter=100, tol=1e-3)
    model.startprob_ = start_probability
    model.transmat_ = transition_probability
    model.emissionprob_ = emission_probability
    logprob, box = model.decode( np.array([obs]).T, algorithm="viterbi")
    print('MultinomialHMM viterbi算法')
    print([states[i] for i in box])

    print('实现viterbi算法')
    _hmm = HMM(transition_probability, emission_probability, start_probability)
    hiddens=_hmm.viterbi(obs)
    print([ states[i] for i in hiddens])
if __name__ == '__main__':
    decode()

用hmmlearn库验证我们实现的维特比方法，得到如下结果：

三、学习问题

学习问题仅知道隐藏状态的个数，不妨为N个，通过观察结果求出参数集合:

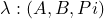
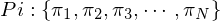
Baum-Welch算法解决学习问题，Baum-Welch算法本质是EM算法(期望最大化算法)：通过E、M步骤迭代得到最优解，其中E步求出目标函数的下界函数，M步求出下界函数本轮最大值，当误差小于设定值后得到最优解，详细算法参见EM算法详解。当每个时刻的隐藏状态已知、观察结果为T个,HMM的观察结果概率可表达为：

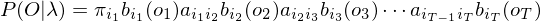
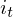代表每个时刻隐藏状态的序号，下标数字代表时刻，显然有：

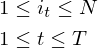
学习问题中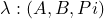未知、且每个时刻隐藏状态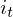也是未知的，用I表示所有隐藏状态可能性的集合：

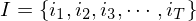
由加法原理知，此时观察结果的概率为：

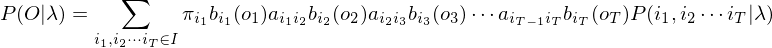
上式取对数后得到函数f(λ):

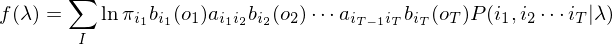
根据Jesson不等式，可得函数f(λ)的下界函数Q(λ)：

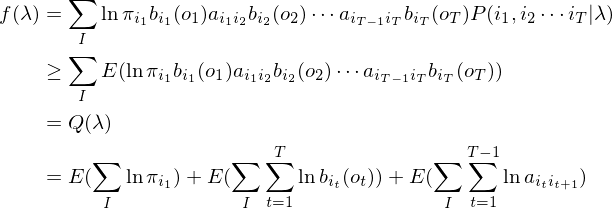
根据数学期望公式，下界函数Q(λ)可以进一步展开：

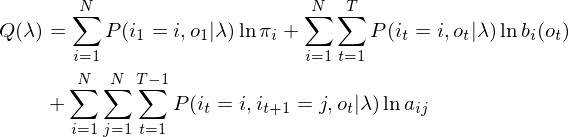  (3.1)

以上是EM算法的E步骤，得到最大似然法函数f(λ)的下界函数Q(λ)。接下来通过M步骤，对公式(3.1)求导得到本轮参数集合λ的最优解。EM算法随机会初始化λ值，不妨设初始化参数集合为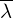，引入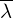后公式(3.1)中以下三个元素都是常数：

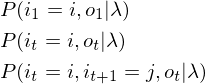
此时下界函数Q(λ)有以下形式：

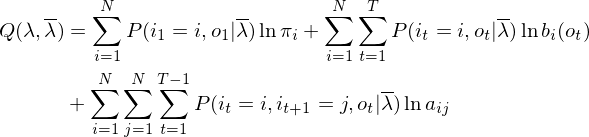    (3.1.1)

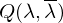函数中分为三部分，分别是初始概率矩阵、发射概率矩阵、转移概率矩阵，这三者之间是相互独立的，分别求出这三部分最值，也就得到了函数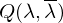最值。

3.1 初始状态概率Pi

先求初始概率矩阵Pi，目标函数为：

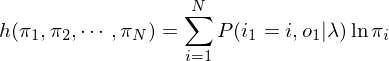
另有约束条件：

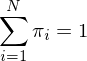
利用拉格朗日乘数法得拉格朗日函数：