背包问题(Knapsack problem)是一个动态规划问题，假设有n种货物，每种货物的的价值是v[i],重量是w[i],需要在背包负载有限的前提下求出具有最大货值的组合（策略），使用暴力算法也可以求出背包问题最优解，而利用动态规划可以将算法的复杂度降至接近于多项式复杂度，背包问题根据每种货物的数量限制可分为以下几种：

0-1背包问题：每种货物数量1件，选择每种货物的策略是取(1)还是不取(0)。

完全背包问题：每种货物数量有无限个，最终的策略是每种货物取多少件。

多重背包问题：每种货物的数量为有限个，且各种货物数量不一样，比如第i种货物的数量为a[i]件。

解决了完全背包问题后，通过引入数量的判断条件，就可解决其他两种背包问题。介绍背包问题算法之前先来了解一些动态规划的相关知识及术语。

一、动态规划

1.1、概念介绍

    线性规划为静态规划，而动态规划显著的特点是问题有阶段性，以下面的最短路线问题为例：

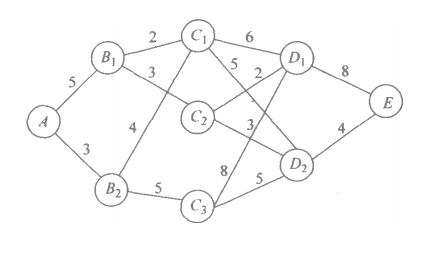
上图中圈号代表具体的地址结点，两个结点间连线代表两地距离，最短路线问题需要求出，从出发点A到目的地E哪条路径最短。上图到达目的地可分为四个阶段，A出发选B₁或B₂为第一阶段，从B_i到C_i为第二阶段，C_i到D_i为第三个阶段，D_i到E为第四个阶段；圈内字母代表状态，每个阶段初始状态集合称为该阶段的状态，例如第一阶段状态S₁={A}，第二阶段状态S₂={B₁,B₂},第三阶段状态S₃={C₁,C₂,C₃},第四阶段状态S₄={D₁，D₂},每个阶段向下一个阶段前进时，面临着多种选择,如第一阶段向第二阶段变化时可选择A到B₁或A到B₂,每一种选择称为决策，决策产生新的状态用小写s表示，而每个阶段决策用小写u表示，例如选择从A到B₁则有s₂=B₁，而选择从A到B₂则有s₂=B₂，状态s_k结合决策u_k，下个阶段k+1状态往往是能确定的，称s_k+1=T(s_k,u_k)为状态转移方程。从A到E每个阶段选择不同的决策构成一个状态序列p_1,n(s₁)称为策略，从k阶段开始策略称为子策略用p_k,n(s_k)表示，显而易见，从出发点A到目的地E有许多种策略。

    以上介绍了动态规划中状态、决策、状态转移方程、策略的概念，接下来再看与策略优化相关的概念，对于最短路线问题而言，最优的策略显然要求各个阶段路程之和最小。假设在k阶段状态为s_k，采用了决策u_k后得到k+1阶段的状态s_k+1,用一个阶段指标函数来量化决策u_k，例如从A到B₁节点有：

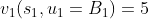
与此类似，如决策采用A到B₂节点则有：

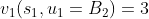
假设k阶段状态为s_k，采取策略p_k,n(s_k)产生的一系列阶段函数之和称为指标函数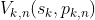：,具体形式为：

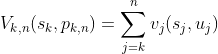
从k阶段的状态s_k到最终状态s_n有许多策略可用，就最短路线问题而言，最优的策略显然是指标函数值最小的策略，引入最优指标函数f_k(s_k):

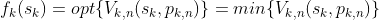
动态规划问题归结为求解最优指标函数f₁(s₁)，得到f₁(s₁)后即可得到最优策略。

1.2、逆推法

    求解动态规划常用方法有逆推法和顺推法，设动态规划问题一共有n个阶段，逆推法从n阶段向前逆向推导每个阶段的最优决策，直至推导出最优指标函数f₁(s₁),然后利用已推导的最优决策，从开始阶段顺次得到各个阶段最优状态。以开头最短路线问题为例：

从E点出发即k=4时：

针对D₁有指标函数f₄(D₁)=8,状态转移方程E=T(D₁,u₄(D₁)),针对D₂有f₄(D₂)=4,状态转移方程E=T(D₂,u₄(D₂))。

 k=3时：

f₃(C₁)=min{6+f₄(D₁),5+f₄(D₂)}=min{6+8,5+4}=9,从C₁出发到下个阶段最优决策是选择D₂，记u₃(C₁)=D₂，在确保最短短路程的前提下，有状态转移方程D₂=T(C₁,u₃(C₁))_。

_{f3(C2)=min{2+f4(D1),3+f4(D2)}=min{2+8,3+4}=7,记u3(C2)=D2。} 

_{f3(C3)=min{8+f4(D1),5+f4(D2)}=min{8+8,5+4}=9,记u3(C3)=D2。}

k=2时：

f₂(B₁)=min{2+f₃(C₁),3+f₃(C₂)}=min{2+9,3+7}=10,记u₂(B₁)=C_2。

f₂(B₂)=min{4+f₃(C₁),5+f₃(C₃)}=min{4+9,5+9}=13,记u₂(B₂)=C_1。

k=1时：

f₁(A)=min{5+f₂(B₁),3+f₂(B₂)}=min{5+10,3+13}=15,记u₁(A)=B₁

得到最优指标函数f₁(A)后即得到了问题最优值，接下来再从A出发，利用每个阶段的最优决策求出每个阶段的状态：

k=1时，由u₁(A)=B₁，确定路线A到B₁。

k=2时，由u₂(B₁)=C₂，确定路线B₁到C₂。

k=3时，由u₃(C₂)=D₂，确定路线C₂到D₂。

k=4时，由u₄(D₂)=E，确定路线D₂到E。

综上所述，该动态规划最优路线为A→B₁→C₂→D₂→E。

1.3、顺推法

    顺推法顾名思义是从k=1阶段开始顺序推导至k=n阶段，首先引入一个新的最优指标函数：

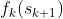
上式中k表示第k阶段结束状态为s_k+1时最优函数，仍以上图为例:

C₁同时连接B₁和B₂，B₁、B₂是第一阶段结束状态可选集合，同时B₁、B₂又是第二阶段开始状态集合；而C₁属于第三阶段开始状态也是第二阶段结束状态之一。根据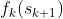定义有：f₂(C₁)=min{2+f₁(B₁),4+f₁(B₂)},逆推法的最优指标函数以开始状态作为标识，而顺推法的最优指标函数以结束状态作为标识，选择的标识不同是因两者算法差异造成的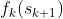，用公式可表达为：

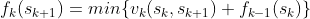 ①

①式中s_k是一个变量，s_k+1是一个定值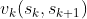，表示状态s_k与s_k+1之间的阶段指标函数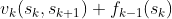，表达的是一个集合，公式中含义可根据f₂(C₁)的表达式对号入座来理解，特别的，设初始状态f₀(s₁)=0。顺推法求解上面最短路线问题即为求解最优指标函数f₄(E)，接下来用顺推法解决之前的最短路线问题。

k=1时，有

f₁(B₁)=5,u₁(B₁)=A;f₁(B₂)=3,u₁(B₂)=A

k=2时，有

f₂(C₁)=min{2+f₁(B₁),4+f₁(B₂)}=min{2+5,4+3}=7,u₂(C₁)=B₁或B₂

_{f2(C2)=min{3+f1(B1)}=8，u2(C2)=B1}

_{f2(C3)=min{5+f1(B1)}=8，u2(C3)=B2}

_k=3时，有

_{f3(D1)=min{6+f2(C1),2+f2(C2),8+f2(C3)}=min{6+7,2+8,8+8}=10}

_u3(D1)=C2

f₃(D₂)=min{5+f₂(C₁),3+f₂(C₂),5+f₂(C₃)}=min{7+7,3+8,7+8}=10

_u3(D2)=C2

k=4时

f₄(E)=min{8+f₃(D₁), 4+f₃(D₂)}=min{8+10,4+11}=15,u₄(E)=D₂

注意到顺推法得到的最优指标函数f₄(E)等于逆推法得到f₁(A),这是很容易理解的，A到E等效于E到A，而由决策序列：

u₄(E)=D_{2 ，}u₃(D₂)=C₂ ，u₂(C₂)=B_{1 ，}u₁(B₁)=A 

可知最优策略为A→B₁→C₂→D₂→E。

    可根据目标最优指标函数来区分使用的是逆推法还是顺推法，如目标函数是形式f₁(A)，即以初始状态和初始阶段为最优指标函数标识符的，使用的是逆推法；而类似f₄(E)以最终阶段和最终状态为函数标识符的是顺推法。

二、动态规划解决背包问题

2.1、完全背包问题

    前面介绍过，完全背包问题指的是每种货物数量不限，以下面这个问题为例，假设一辆汽车最多可运7吨货物，有甲、乙、丙三种物资，每种物资货值及重量如下表：

要求出在规定核载吨位下最大货值的组合。

上述问题可转化为下面的动态规划问题：

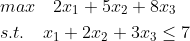
x₁,x₂,x₃都是件数、皆为整数。对物资甲、乙、丙分三阶段分配数量，起始状态s₁≤7代表待分配吨位不大于7吨，x₁,x₂,x₃件数作为决策变量，分配完物资甲后第二阶段初始状态s₂=s₁-x₁,与此类似，分配完物资乙后第三阶段状态s₃=s₂-2x₂,分配完丙后s₄=s₃-3x₃=0，有了状态转移方程之后引入最优指标函数f_k(s),其意义指在装载能力不大于s的前提下，k阶段到最后第3阶段的最大货值，显然f₁(7)的值即为所求的最大货值，由目标最优指标函数形式可知，将使用逆推法求解该问题,f₁(7)表达式为：

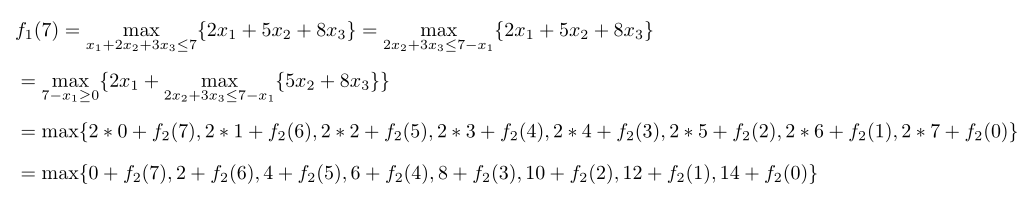
f₁(7)中根据状态转移方程s₂=s₁-x₁确定了第二阶段可分配重量，接下来逐个分析其中多项式，以f₂(7)为例，f₂(7)代表在第一阶段货物甲分配了0件：