线性回归有许多方法可以解决，比如最小二乘法、神经网络等，本篇介绍基于线性代数,利用向量、线性空间、子空间概念快速求解线性回归问题，掌握本章知识点后可以利用有些结论解决如函数逼近问题。

  一、线性空间、子空间

  将有限个基通过数乘、加操作张成线性空间，线性空间中可以最多可以用n个线性不相关的基张成，就可以说这个线性空间是n维的，如果一个线性空间有n个基分别是α₁,α₂,α₃...α_n，这个线性空间可以这样表达:space=span{α₁,α₂,α₃...α_n}。注意空间的维度和向量的维度不一样，向量维度是指向量中元素的个数，比如向量v=(1,2,3)^T代表了一个维度是3的向量，空间的维度是指有多少个基组成了这个空间，空间的基本身也是一个向量。

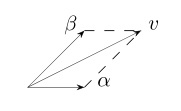
   如果我们手上只有一个子空间，怎么拓展子空间从而能够表示整个空间里的任意一个向量？结合上面例子，只有一个子空间W，即XOY平面，怎么拓展XOY平面去表示一个三维空间里的任意一个向量。其实很简单，再加入一个向量进来，联合XOY平面就是三维了。具体做法是，在XOY平面外任选一点，从该点做一条垂直于XOY平面的直线，这个直线就是我们所需要的向量， 效果如下图：

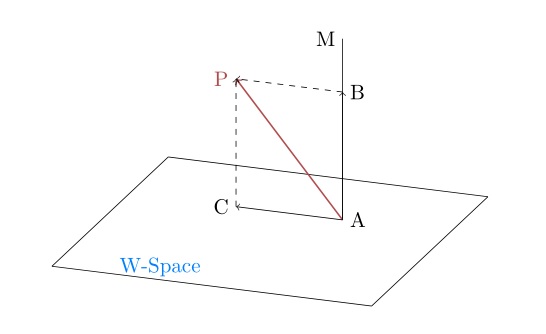
    可以看到，在线性空间任意一个向量AP都可以用W子空间里的一个向量AC和新引入向量AB线性组合，而AC代表子空间里一个向量，向量AC又可以用W子空间的基线性组合，W子空间是二维的，实际应用中不管W子空间是多少维的，由于其中任意一个向量都可以用子空间的基线性组合来表示，常把W子空间抽象成一个平面，也叫超平面。需要强调的是：

1)、新引入的AM向量也是三维空间的一个子空间。

2)、新引入的AM可以任选一条不在XOY平面直线，不在XOY平面内意味着与XOY平面的两个基线性不相关，这样联合之后复合空间一定是3维的。

3)、向量AC称为向量AP在W子空间的投影，可以发现向量AP与所有在W子空间的向量中，只有与AC是距离最短的，即固定线性空间中一个向量AP，在W子空间找出与其最短距离向量只有AC一个，我们将运用这个性质来实现线性回归。

二、求解未知参数实现线性回归

2.1 回归方程与线性空间的关系

   有了以上的知识储备后，我们就可以来实现线性回归，先来表述一下线性回归所要解决的问题。

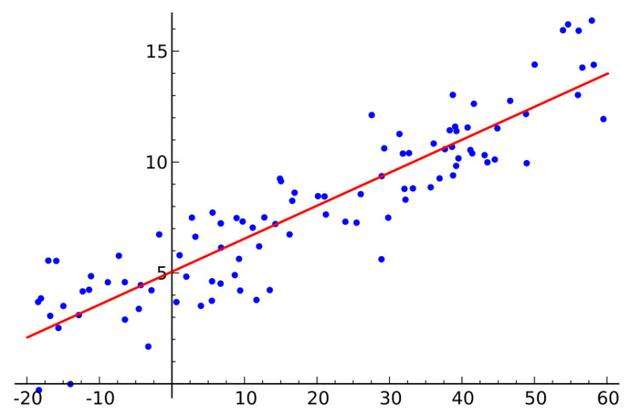
这里的红色直线就代表待求解的回归函数，本例中这是以身高和年龄为自变量的函数，蓝色点代表真实体重信息，显然在真实的世界里，蓝色点不会规规矩矩的在一条直线上，即收敛在红色的这条直线上，这里只能是"约等于"，下面结合之前介绍的知识来求解未知参数a,b,c。

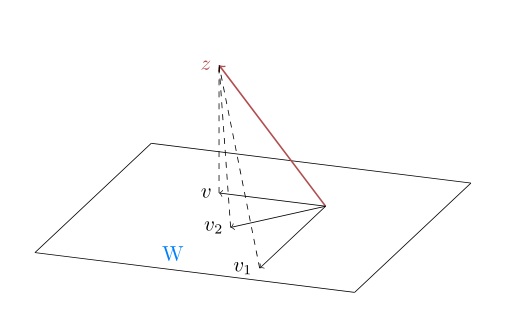
在W平面里虚线代表了不同向量与z之间的误差，只有z在W平面的投影v最短，求出v的过程就是求未知参数a,b,c的过程,在求解之前先来了解一下线性代数中投影的概念。

2.2 投影矩阵

    首先来看两个向量之间投影，如下图所示：

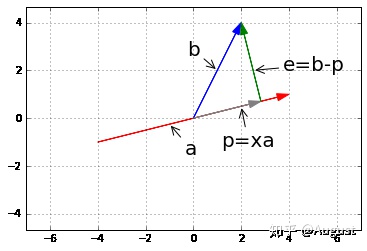
向量b在a上的投影为p=ax,x ∈R,而向量e=b-p,e一般称为误差，向量e和a正交，即有等式：