傅里叶变换是用三角函数表示目标函数，傅里叶变换广泛的应用在信号处理、偏微分方程、热力学、概率统计等领域：大到天体观测，小到我们手机中图片、音频应用等，没有傅里叶变换就没有如今丰富多彩的信息化时代。在人工智能领域中，可利用傅里叶变换证明中心极限定理，而中心极限定理是概率学最重要的基石；傅里叶变换本质是将时域的信息汇总到频域中，当两组数据的傅里叶变换结果相同时，称为两者依概率收敛。本章介绍傅里叶变换推导过程并结合代码实现傅里叶变换，按数学推导的离散傅里叶变换算法复杂度较高，本章最后介绍快速傅里叶变换（FFT）的实现原理。

一、傅里叶变换原理

1.1 目标函数f(x)为周期2π的函数

前面的章节中曾用多项式拟合目标函数，傅里叶变换是利用三角函数拟合函数，正弦、余弦函数有以下性质：

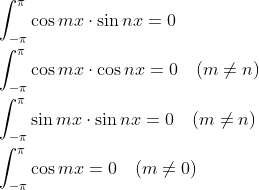 (1)

三角函数集合在[-π,π]可以看成函数空间一组正交基,目标函数f(x)可写成傅里叶级数：

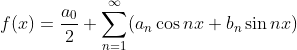 （1.1）

a_n、b_n都是待定系数，也表示f(x)在正交基上的坐标，(1.1)式两边乘以cos mx ，m为一个特定系数坐标，求积分有：

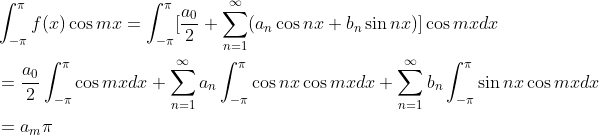
由此可得a_n:

    (1.3)

同样可得b_n:

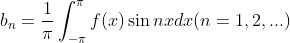      (1.4)

上面函数f(x)周期为2π，如果f(x)是周期为2T，可用线性仿射将f(x)的定义域x投射到t上，t的周期是2π:

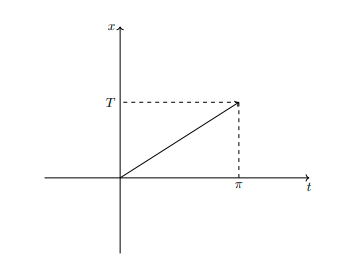
此时有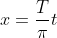,,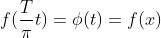从上图可见，Φ(t)是在[-∞,∞]一个周期为2π函数，有：

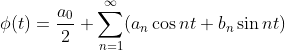
将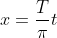转化为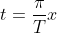代入上式可得：

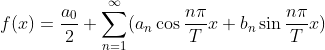 （1.5）

再利用积分求系数a_n、b_n：

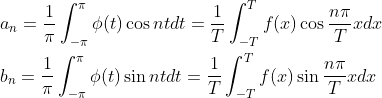  （1.6）

1.2 f(x)非周期函数

f(x)不是周期函数时，可理解为f(x)的周期为+∞，不妨先考虑周期为2T函数f_T(x)，T为无限大取极限后，可将f_T(x)延拓到周期为+∞函数f(x)，先利用欧拉公式将公式(1.5)变为复数形式：

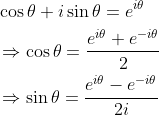
设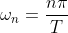公式(1.5)可表示成：

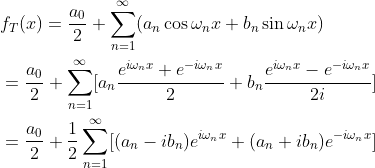     (1.7)

a_n+ib_n和a_n-ib_n是一对共轭复数，幅值相同，相位角在x轴上对称，设c_n=a_n-ib_n,利用公式(1.6)得：

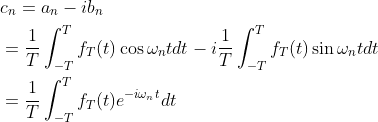    (1.7.1)

c_n的共轭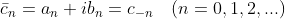且有：

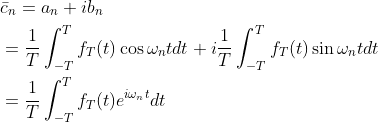  (1.7.2)

公式1.7中n的取值范围是从1到无穷，引入c_n后n的取值范围是(-∞,+∞)，1.7式写成下面的形式：

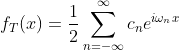   (1.7.3)

1.7.1代入上式后得到f_T(x)：

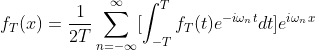   (1.8)

接下来利用式(1.8)将f_T(x)周期延拓至∞可得目标函数f(x):

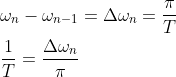    (1.8.1)

式(1.8.1)代入(1.8)得到f(x)极限形式的函数：

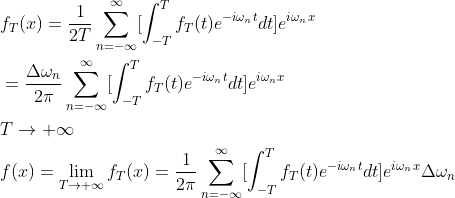
当T为+∞时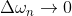，,f(x)此时可表示成积分形式：

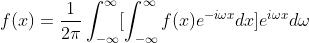 （1.9）

上式中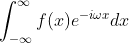称为原函数f(x)的傅里叶变换，计算积分过程中ω视为符号常量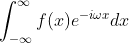，积分结果是含自变量ω的函数,傅里叶变换可用下面的表示方式：

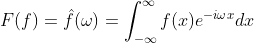 （1.10）

而F(f)再经过一次积分后可还原为f(x),这称为傅里叶逆变换：

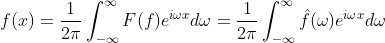
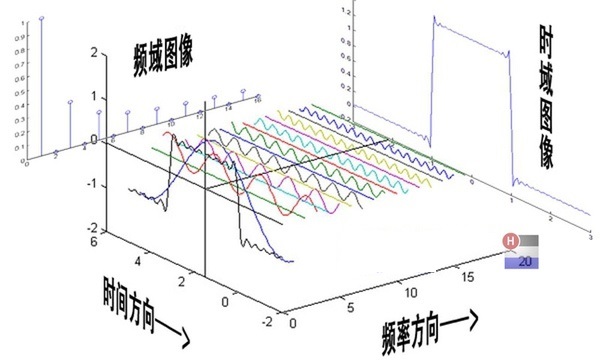
f(x)同样称为时域函数，比如记录每天雨量的变化、每小时道路车辆的流量、汽车每年的里程数等，时域函数是日常生活中大量接触到的函数模型，而1.10式将f(x)经过傅里叶变换后得到是频域的信息，频域单位是赫兹，反应出原函数周期性方面的信息，时域与频域观察世界视角不同，可以用下图来加强对两者的认识。

二、程序实现傅里叶变换

2.1 离散傅里叶变换

代码中利用式(1.10)的离散形式实现傅里叶变换,设在定义域内选择N个数据实现f(x)函数离散化，f(x)可表示成：

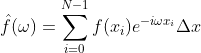 （2）

如果f(x)表示的是一个信号，所选择的时间段为一秒即单位时间，那么N称为采样频率，由采样定理可知，采样频率至少是信号最大频率的2倍，就傅里叶变换而言，采样频率最好是2的整数倍，有了这些设定后公式（2）可表示为：

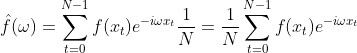    (2.1)

上式用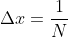将单位时间一秒分成N份，在傅里叶变换中也称归一化，2.1式中ω代表角速度，通常将角速度处理成频率形式，频率h与角速度的关系有：

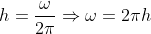
上式代入2.1后有：

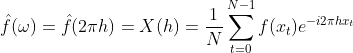  （2.2）

X(h)是单位为赫兹的频域函数，再回头看公式1.7.3，参数c_n中的n取值范围是(-∞,+∞),也就是说原公式中是允许有负角速度或者说负频率存在的，而(2.2)式中n是非负整数，代表着客观物理世界中没有所谓的负频率，这是数学与物理的差异性导致的，(2.2)引入负频率才能满足傅里叶变换公式，幸运的是正频率与负频率是共轭的关系，即c_n与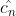关系，两者的幅值是一样的，傅里叶离散变换的目标是得到每个频率对应幅值，所以将（2.2）乘以2即可得到与1.7.3式一样的定义。

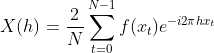      (2.3)

下面代码利用公式2.3实现傅里叶离散变换，目标函数(原始信号)为：

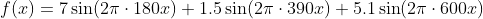
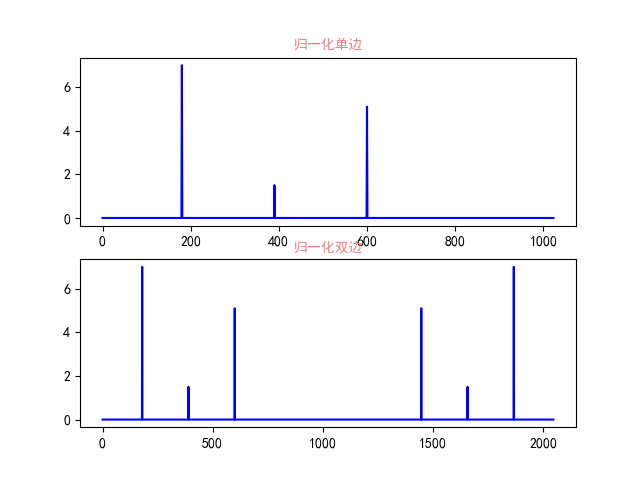
原始信号含有频率为180、390、600Hz的信号，采用频率为2048Hz,对应幅值分别为7、1.5、5.1。

import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 显示负号
Samplingfq=2048
def loadsignal(N  ):
    # 采样点选择1400个，因为设置的信号频率分量最高为600Hz，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400Hz（即一秒内有1400个采样点）
    x = np.linspace(0, 1, N)
    # 设置需要采样的信号，频率分量有180，390和600
    y = 7 * np.sin(2 * np.pi * 180 * x) + 1.5 * np.sin(2 * np.pi * 390 * x) + 5.1 * np.sin(2 * np.pi * 600 * x)
    return  x,y
 

def FourierTransform():
    x, y = loadsignal(Samplingfq)
    ffts=[]
    for i in range(Samplingfq):
        real=0
        imag=0
        for t in range(Samplingfq):
            real=real+y[t]* np.cos(2*np.pi*i*x[t])*2/Samplingfq
            imag=imag+y[t]*  np.sin(2*np.pi*i*x[t])*-2/Samplingfq
        ffts.append([i,np.sqrt(real**2+imag**2)  ])
    ffts=np.array(ffts)
    plt.subplot(211)
    plt.plot(range(int(Samplingfq/2)),  ffts[:int(Samplingfq/2),1]  , 'b')
    plt.title('归一化单边', fontsize=10, color='#F08080')
    plt.subplot(212)
    plt.plot(range(Samplingfq),  ffts[:, 1]  , 'b')
    plt.title('归一化双边', fontsize=10, color='#F08080')
    plt.show()


if __name__ == '__main__':
    FourierTransform()

 for i in range(Samplingfq):
        real=0
        imag=0
        for t in range(Samplingfq):
            real=real+y[t]* np.cos(2*np.pi*i*x[t])*2/Samplingfq
            imag=imag+y[t]*  np.sin(2*np.pi*i*x[t])*-2/Samplingfq

上面代码片段即为对公式2.3应用，傅里叶离散变换后得到频率图如下图所示：

2.2 快速傅里叶变换FFT

上面的示例程序复杂度是n²,n对应于采样频率，当目标函数或原始信号的最大频率较高时，根据采样定理，采样频率至少为最大频率的2倍，这就造成n²值非常大，算法复杂度较高影响傅里叶变换的使用，利用快速傅里叶变换(FFT)可将复杂度降至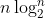,随着采样频率的升高，FFT效率提升越来越明显，FFT是信号传输、图像分析、频谱分析、数据压缩最重要的数据算法之一，FFT出现给傅里叶变换带来了旺盛的生命力。

单位时间内采样频率为N，0到N-1之间任意时刻t信号值用x(t)表示，2.3式用下式表示：

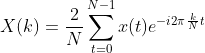 (2.4)

上式中k代表0到N-1之间任意一个频率，且有0<=k<N-1,引入一个新的符号变量：