函数梯度与隐函数
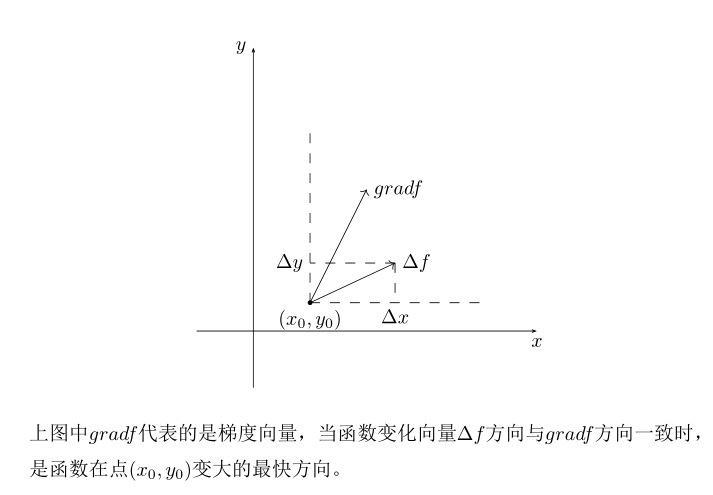
梯度是函数的定义域中的一个向量,该向量指向的方向是函数值变大的最快方向,相应的,梯度的反方向则是函数变小的最快方向,与梯度配合使用的是函数的等值线,从几何角度来说,梯度是两条等值线之间指向最短距离的一条向量,最优化问题中常需要使用梯度来求函数的最值。本篇通过介绍梯度、隐函数、函数最值几个方面来理清其中的关系,并对容易混淆的地方做详细的解释,本篇中很多知识点都可以在数学分析教材中获得,将梯度单独作为一篇是为了以后讲解其他算法时可以方便引用,有基础的读者可以略去不看。
一、梯度的概念
梯度是一个向量,从物理学角度说向量是一个有大小和方向的矢量,从数学角度来看向量是一个线性空间中的元素,可以通过这个线性空间的中的基线性组合表示出来,在计算机算法中梯度更像是一个导航软件,指引着算法找到目标最小值或最大值。

z=f(x,y)是三维空间的一个曲面,设点P0=(x0,y0,z0)是三维空间的一个点,经过P0点有无数条属于该曲面的曲线,这些曲线在P0点的切线有无数条,这些切线构成一个切平面,曲面在P0点可以近似的用这个切平面表示,以上讨论的曲面、曲线、切线、切平面都在三维空间中,而P0点的梯度则在定义域的二维空间中,与梯度相关的是函数的等值线,如下图:
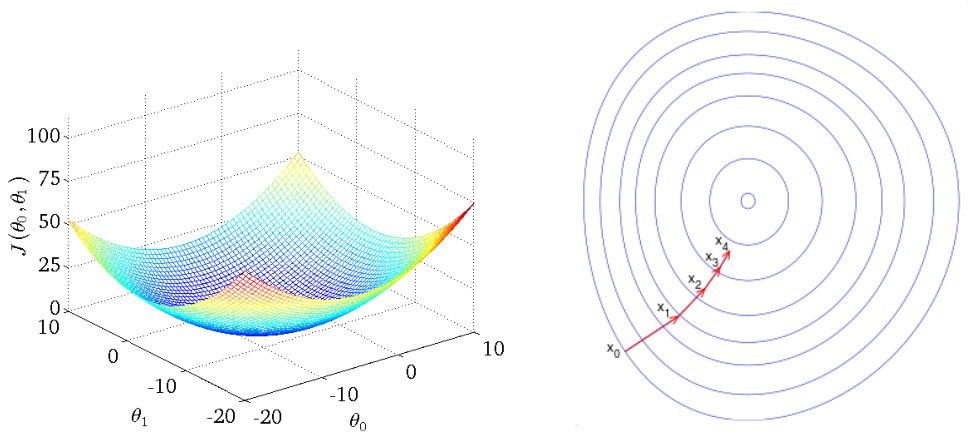
上图左侧是一个三维空间的曲面,右侧是其二维定义域空间的等值线,每个圆环代表函数等值线,其意义是函数值相同的点投影到定义域的曲线,等值线上一系列的红色向量即为梯度,沿着梯度可以到到达函数最值点。
二、隐函数及其梯度
2.1 隐函数的定义
上面的函数z=f(x,y)将应变量z分离出来,表示为两个自变量x,y的函数,这样的函数称为显函数,反映出是一个三维空间的曲面,如果设z=0即得到f(x,y)=0,f(x,y)=0的函数是原函数z=f(x,y)坍塌到二维空间XOY(降低了一个维度),也可以认为f(x,y)=0是原函数z=f(x,y)与平面XOY相交形成的一个曲线,f(x,y)=0函数并没有将应变量与自变量分离,这种函数形式称为隐函数。在最优化应用中,常利用KKT条件把不等式约束转化为等式约束,而等式约束条件又通常写成隐函数的形式,如何将隐函数f(x,y)=0的自变量与应变量分离出来,比如写成y=h(x)这个形式需要用到以下定理:
隐函数存在定理:如果在点P0:(x0,y0)处,有f(x0,y0)=0;fy(x0,y0)╪0,在该点则有微分形式:dy/dx=-fx/fy。
以上定理中fx是对函数f(x,y)求关于x的偏导数,fy也以相同方法处理,这样可以得到dy/dx的函数关系式,进一步积分即可得到y与x的关系。所以 隐函数定理也可以简略的说点P0:(x0,y0)处,有f(x0,y0)=0;fy(x0,y0)╪0,则y可以表示为x的函数,这就将自变量与应变量分离出来变成了一个显函数。本篇不详细证明隐函数存在定理,并且上面的表述没有加入函数连续性的约束,如有兴趣朋友可以参考数学分析等书籍。
| 上一篇 利用线性空间、子空间实现线性回归问题 | 下一篇 基变换、线性变换与pca主成分分析 |
| 评论区 | |