前面介绍的决策树ID3，C4.5是多叉树，CART树是一个完全二叉树，CART树不仅能完成分类也能实现回归功能，所谓回归指的是目标是一个连续的数值类型，比如体重、身高、收入、价格等，ID3，C4.5其核心是信息熵的应用，而在实际应用中,熵的运算会涉及大量的对数运算，复杂度还是比较高的。CART树采用了一个与熵近似的概念'基尼系数',不同于熵来自于物理学，基尼系数来自于经济学范畴，基尼系数原本是用来衡量国民收入是否平均：当基尼系数为0时代表收入平均，而大于0.5时代表贫富差异显著。在决策树模型中，基尼系数越高代表信息纯度越低，基尼系数越低代表纯度越高，而纯度的高低代表样本数据不确定性的大小，这方面来说基尼系数与熵的功效一致，实际上基尼系数在是信息熵的近似，可以观察下图:

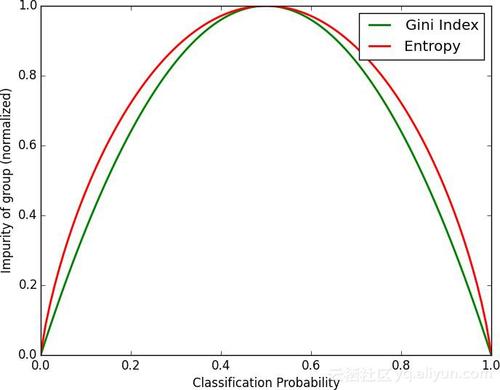
上图中红色曲线代表信息熵，绿色曲线代表基尼系数，可以看到两者走势是一样的。基尼系数是初等函数二次多项式的运算，这比熵的对数运算简单多了。CART树能不能用熵来代替基尼系数呢？答案是当然可以了，熵更能反映出信息的不确定性，但是接下来了解算法特性后就会发现，如果用熵来构建CART树，计算量将会非常之大，选用基尼系数是平衡准确率与效率之后的折中之举，这个折中的办法其实不会降低CART树的实际效果，在介绍ID3，C4.5结尾时曾提到，决策树本质是一个弱分类器，实际应用中不会单独用一棵决策树来实现分类，而是会用集成算法将多棵决策树汇总起来进行运算。集成算涉及相关知识有Bagging，Boosting 等，可参考本站文章bagging，adaboost原理。

一、CART树实现分类

2.1、CART树分类原理介绍

前面已经说过，CART树利用基尼系数代替信息熵表示信息的不确定性，CART树实现分类的原理与ID3，C4.5一样，分别计算各个属性对降低基尼系数高低作为分裂决策树结点的依据，与ID3，C4.5不同的是CART树是一个二叉树，对结点分裂时会选择一个切分点，将一个属性的值分成两类分别计算，分成两类的过程代表二叉树子树的两个分支。

    CART树实现分类过程中每选择一个属性计算条件基尼系数时，都需要遍历整个属性值找到最佳切分点，然后再类似重复计算其他属性的条件基尼系数，择其最优的作为决策树结点，可以看到这个计算量比起ID3，C4.5是成倍上升的，所以CART树选择一个成本较低的二次函数而不是对数函数作为数学模型。综上所述，每个属性寻找最佳切分点是CART树与ID3，C4.5最大不同之处。

    另外需要注意的是，前面在提到C4.5对ID3改进时，其中有一点，ID3偏好值将多元化的属性优先作为决策树结点，C4.5通过除以属性的信息熵来抵消这方面的偏好；而CART树的条件基尼系数、基尼系数增益其形式都与为ID3的条件熵、信息增益一样，为什么这里就不存在ID3问题呢？或者说CART树是否偏好多元化的属性？其实仔细看一下CART树计算过程可以看到，由于切分点概念的引入，不管属性值有多少，都将所有属性值都划分成两部分，也就是说CART树认为所有的属性值只有两种情况，没有哪个属性能占到多样化这种便宜。

    下面看一个具体的CART树实现分类的例子，这是一个根据是否有房、婚姻状况、收入情况判断是否会拖欠贷款的分类过程，可以看到收入情况是一个数值型的属性，其他两个是离散型属性。

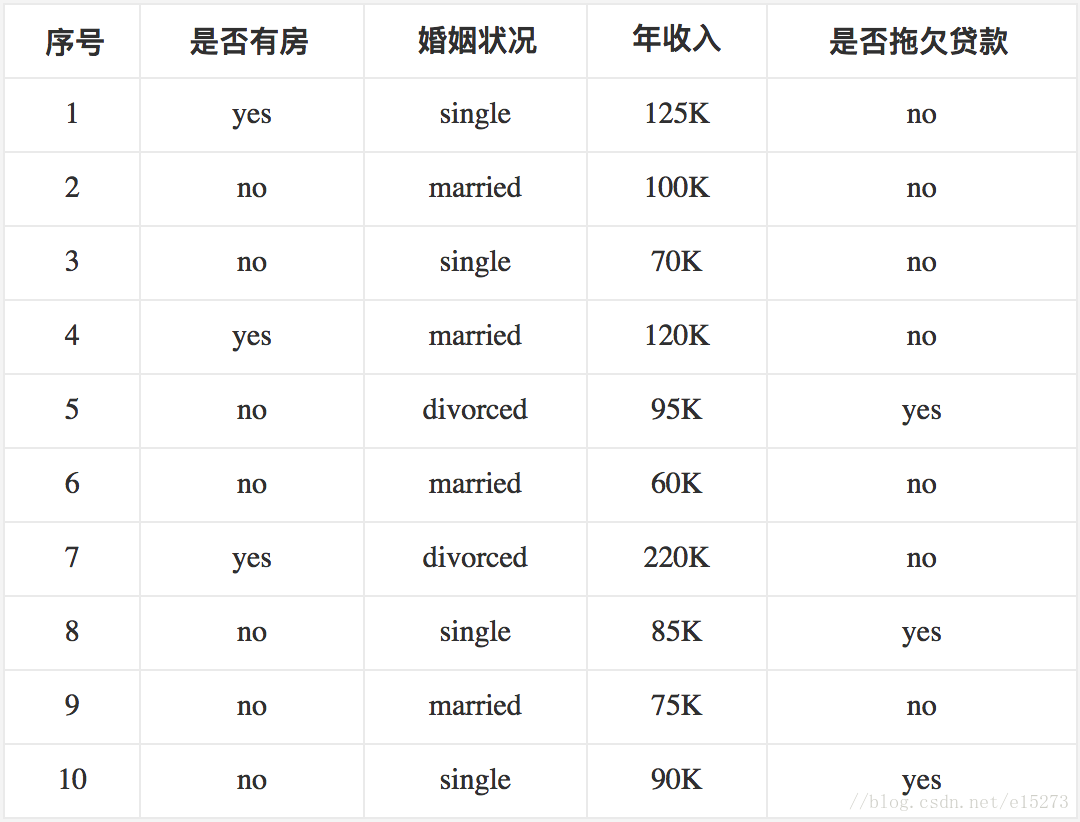
首先计算分类的基尼系数，这里拖欠贷款的有3例，不拖欠的有7例，利用公式(1)可得：

Gini(是否拖欠贷款)=1−(3/10)^2−(7/10)^2=0.42

然后分别计算属性的条件基尼系数，比如是否有房这个属性，由于这个属性本身只有两个分类，所以切分点只要一个即可：

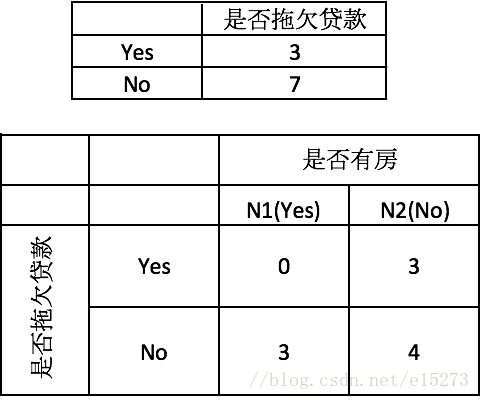
Gini(有房)=1−(0/3)^2−(3/3)^2=0

Gini(无房)=1−(3/7)^2−(4/7)^2=0.4898

Gain_Gini{是否拖欠贷款,是否有房}=0.42−7/10×0.4898−3/10×0=0.077

接下来看婚姻状况，该属性值有三个married，single，divorced，可先选{married} | {single,divorced}计算基尼系数增益为：

Gain_Gini{是否拖欠贷款,{married} | {single,divorced}}

=0.42−4/10×[1-0-(4/4)^2]−6/10×[1−(3/6)^2−(3/6)^2]

=0.42−4/10×0−6/10×[1−(3/6)^2−(3/6)^2]=0.12

移动切分点得到其他两种情况的基尼系数增益：

Gain_Gini{是否拖欠贷款,{single} | {married,divorced}}=0.42−4/10×0.5−6/10×[1−(1/6^)2−(5/6)^2]=0.053

Gain_Gini{是否拖欠贷款,{divorced} | {single,married}}=0.42−2/10×0.5−8/10×[1−(2/8)^2−(6/8)^2]=0.02

可以发现婚姻状况按{married} | {single,divorced}切分时基尼系数增益最大(条件基尼系数最小)，所以选择这个属性值切分，将{married} | {single,divorced}作为婚姻状况对是否拖欠贷款的基尼系数增益。

接下来看收入状况，收入是一个数值型属性，将属性值按从小到大排列,并将排列好相邻的属性值，两两计算平均值，得到相邻中值点如下图：

选择相邻中值点作为切分点，从小到大顺序先选择65K，小于65K即年收入为60K的为一个部分，大于65K是第二个部分，然后统计每个部分样本个数，利用上面的公式即可计算出基尼系数增益，从上图可以看到不同切分点下系数增益最大值是0.12，与婚姻状况的系数增益一样。

    以上计算完成了算法的第一步，接下来根据第二步选择婚姻状况作为决策树的节点，并选择切分点{married} | {single,divorced}作为二叉树的两个分支，将married作为左枝，{single,divorced}作为右枝，其中左枝有4个样本其类别都是no，这时左枝为叶结点不需要再分类；而右枝有6个样本，这6个样本再通过'收入'和'是否有房'两个属性再进行分类，此时剩下的6个样本数据的类别的基尼系数为：

Gini(是否拖欠贷款)=1−(3/6)^2−(3/6)^2=0.5

按是否有房对这6个样本计算系数增益可得：

Gain_Gini{是否拖欠贷款,是否有房}=0.5−4/6×[1−(3/4)^2−(1/4)^2]−2/6×0=0.25

收入情况系数增益表如下图:

最后得到CART树分类图如下所示:

2.2 python实现CART分类与剪枝

    介绍C4.5时说过,不剪枝的决策树是过拟合的，C4.5剪枝算法是引入惩罚因子后，利用子树结点与叶结点之间的误差率，当两者误差率差不多时，剪枝子树结点，用叶结点代替子树从而降低过拟合，当时这个惩罚因子是一个固定的常数0.5，CART树剪枝算法与C4.5大致相同，只不过CART树剪枝算法的惩罚因子不再是一个固定的常数，观察下图，有内部结点t以及以t为根结点的子树T_t:

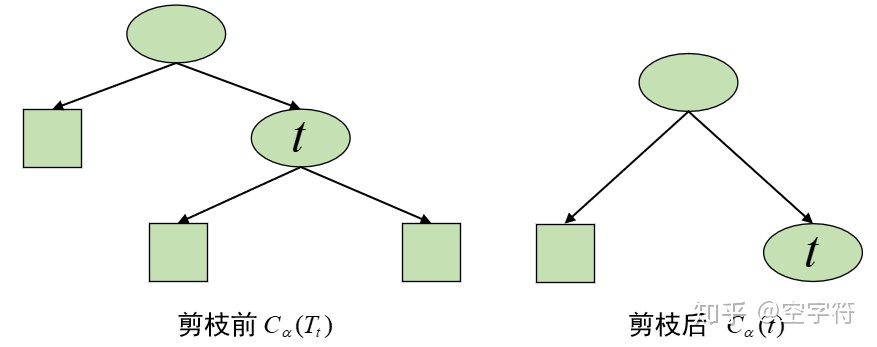
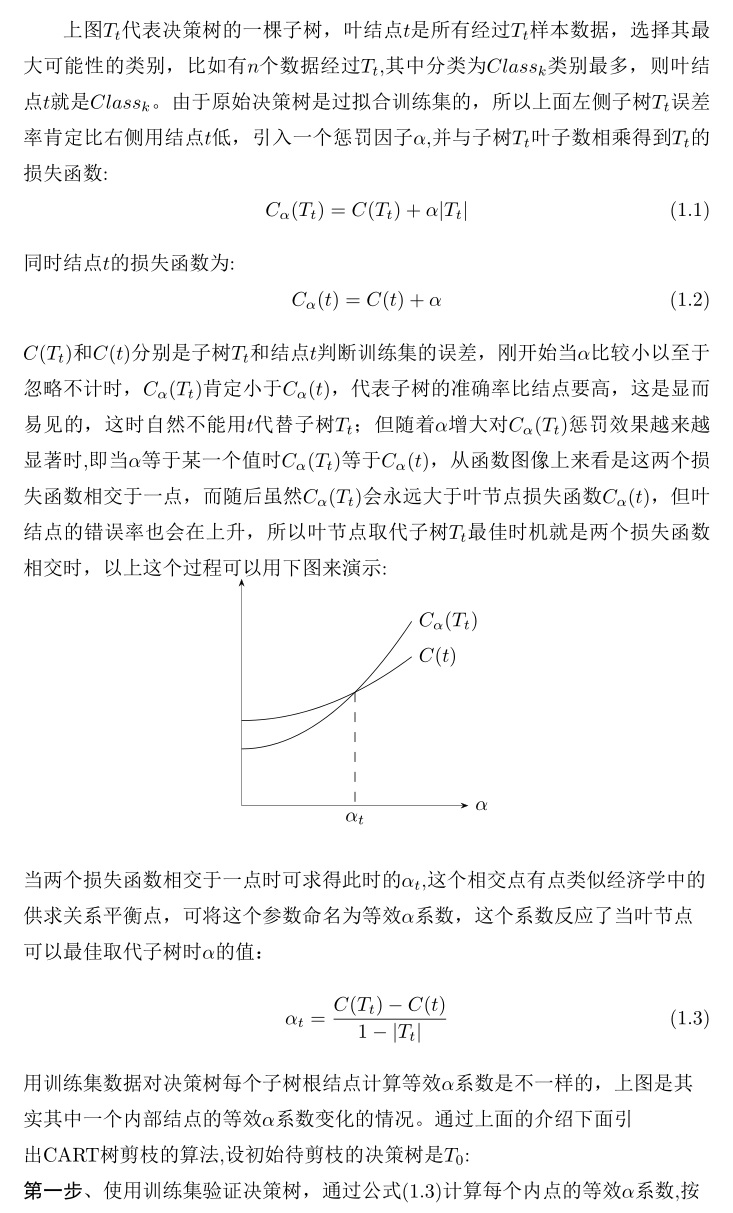
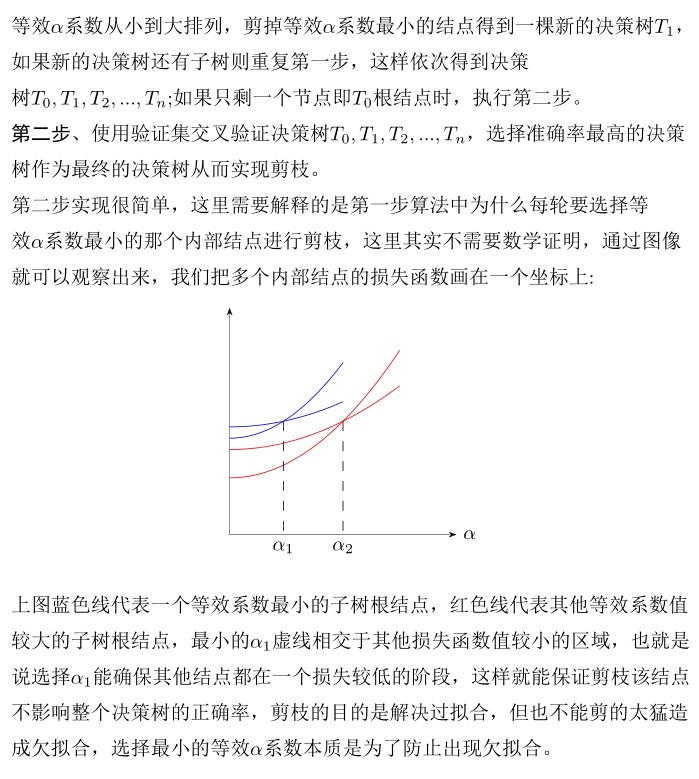
下面python代码实现CART树分类以及剪枝，样本数据是一些二手车数据，属性分别是：'购买时价格','后期保养','车门','装载人数','后备箱大小','安全性'，样本分类是根据以上属性得出的客户购买意向，购买意向主要有以下几类，acc：接受,unacc：不接受,good：好评,vgood:非常好。可以看出属性都是离散型的，适合用基尼系数来实现损失函数。

首先从本站下载样本数据，保存到程序目录下的data目录中:二手车数据。

===treePlot.py===工具类，用于显示决策树代码

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
decisionNode = dict(boxstyle='sawtooth', fc='0.8')
leafNode = dict(boxstyle='round4', fc='0.8')
arrow_args = dict(arrowstyle='<-')
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va='center', ha='center', bbox=nodeType,
                            arrowprops=arrow_args)

# 获取叶子节点数目和树的层数
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr =list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if (type(secondDict[key]).__name__ == 'dict'):
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs

def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if (type(secondDict[key]).__name__ == 'dict'):
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth
def plotTree(myTree, parentPt, nodeTxt):  # if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  # this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr =  list(myTree.keys()) [0]  # the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[
                    key]).__name__ == 'dict':  # test to see if the nodes are dictonaires, if not they are leaf nodes
            plotTree(secondDict[key], cntrPt, str(key))  # recursion
        else:  # it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD

def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    # fig.title("c4.5",size=14)
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)  # no ticks
    #createPlot.ax1.set_title("c4.5", size=24)
    # createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5 / plotTree.totalW;
    plotTree.yOff = 1.0;
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()

===cart.py===cart树实现代码