集成算法AdaBoosting原理
Bagging和Boosting是两种典型集成算法,Bagging的典型算法是随机森林,是利用多种模型进行分类,最后取一个平均值得到最终分类结果,Bagging而言多个模型可以是不同的,Bagging模型的基本原理是平均值可以减小方差,另外一个注意点是Bagging模型适用于小样本的情形,具体Bagging算法会在之后随机森林中详细介绍,本篇主要介绍Boosting算法,主要是选择Boosting中典型AdaBoosting,即提升的Boosting算法。
一、认识了解AdaBoosting算法的过程
AdaBoosting集成的每个分类器都是一样的,每个分类器对特定范围的数据有较高的准确率,有些不能正确分类放到下一轮,并提高分类错误数据的权重,提示下轮分类器重点关注本轮识别错误的数据,从而实现分类器能力的提升;经过若干轮之后,将得到一组分类器,将数据输入这组分类器后会得到一个综合且准确的的分类结果。对于AdaBoosting而言有个形象的比喻,所谓“三个臭皮匠,顶上诸葛亮”,这里的臭皮匠可以理解为每个具体的分类器,也许识别一定范围的数据比较弱,但是多个这样的分类器相互补充,最后会变成一个强分类器(变成诸葛亮)。

以上图显示了每个分类器工作过程,其中打钩的代表分类正确,打叉的代表分类错误。经过M轮后得到一个强分类器,这个分类器几乎能100%将数据正确分类,每个分类器在实际应用中可以是一个神经网络或者是决策树,本篇的分类器以一个简单的分类函数为例,每组分类函数通过设置不同阈值将数据分类,例如数据大于阈值则代表分类一,用随机变量-1表示;小于阈值则代表分类二,用随机变量1表示,下图是一个简单分类器的具体实现细节:
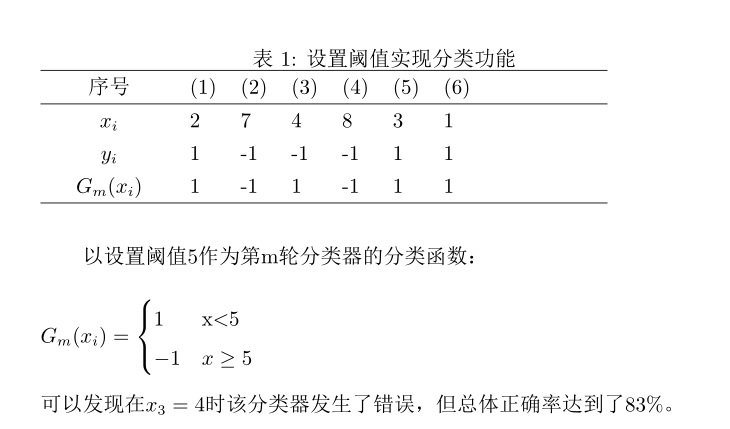
二、AdaBoost算法的原理分析
根据上面的场景介绍,接下来结合数学推导来分析AdaBoosting算法的原理:

我们目标就是求出Gm(x)和αm使公式(2.1)取得最小值,在集成算法中Gm(x)代表一个固定的模型,比如决策树、神经网络等,本例中Gm(x)并不复杂,它是设定阈值后输出结果为-1或1的分类函数,首先来确定Gm(x)函数,在求Gm(x)函数过程中可以认为αm是一个常数,且αm大于等于0。
2.1 求解Gm(x)

公式(3.1)中Wi,m含义是每轮分类器各个样本的权重,由于设定第0轮的分类函数f0(xi)=0,代入公式(3)后可知,第一轮时各个样本数据权重是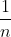 ,权重代入公式(3.1)后,表达式
,权重代入公式(3.1)后,表达式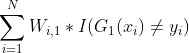 含义是第一轮分类的错误率,每轮过后AdaBoosting算法会根据错误率更新样本权重,比如第二轮后第i个样本权重为:
含义是第一轮分类的错误率,每轮过后AdaBoosting算法会根据错误率更新样本权重,比如第二轮后第i个样本权重为:
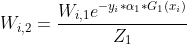 (3.3)
(3.3)
其中Z1是归一化系数,公式为:
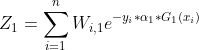
从公式(3.3)可看出,样本的权重与分类函数处理样本的错误率有关:当前一轮某个样本分类错误时,会加大该样本权重传入下一轮分类中,提醒下一轮分类模型重点降低此样本的错误率;与之相反,如果前一轮分类正确则会降低该样本权重传入一下轮,这相当于告诉下一轮模型,此样本已经正确处理,不需要针对该样本再做处理,AdaBoosting正是通过更新权重逐步提升模型准确率的。接下来求αm值,这个值代表每轮分类模型在分类器中的权重,求解αm时可以认为Gm(x)一个定量的函数、或者是一个已知的学习模型。
| 上一篇 决策树(下)-CART树分类、回归、剪枝实现 | 下一篇 EM期望最大化算法 |
| 评论区 | |