Bagging集成算法
前面章节中介绍了Boosting算法,Boosting算法和Bagging算法都是常用的集成算法,集成算法的含义是算法本身用于合并其他模型,比如用Bagging集成决策树可得到随机森林模型,Bagging算法全程叫做Bootstrap aggregating翻译为引导聚集算法。这个缩写含有袋子的意思,也可以理解为放回袋中算法,每次随机抽取一定比例的样本测试某一个模型的准确率,测试完后这批样本放回袋中,测试另外一个模型时,之前的样本可能还会被抽中,最后将多个模型取其平均值或利用投票原则得出一个综合的预测结果。
Boosting和Bagging有以下两个最大的区别,第一、Boosting算法要求所有被集成模型都必须是同一个模型,Bagging算法可以包容多个不同的模型;第二、在Bagging算法集成过程中,多个模型可以并行同时运行,Boosting算法每次都是前一个模型基础进行提升,而Bagging算法各个模型之间没有明显的依赖关系。
Boosting算法适合于小样本数据的处理,比如我们想知道一个鱼塘里有多少条鱼,可以先捕获100条鱼做上标记后放回鱼塘(放回袋中),然后任意捕获10次,每次计算有标记鱼的比例,最后取比例的平均值,比如是0.01,那么鱼塘的鱼总数即可预估为100/0.01=10000条。用这个的办法显然不能去预估一个大海里有多少鱼,因为样本众多,不管前期标记多少鱼,后期每次测试时有标记比例都接近于零。
一、误差、偏差、方差的概念
误差形式有很多种,在介绍CART树实现回归功能时利用了平方误差,其含义是预测数据与实际数据距离,距离值越小模型准确率越高,这三者的关系是误差=偏差+方差,选择、设计一个模型的终极准则是降低误差。

偏差反应预测模型与实际模型之间的距离,偏差反映预测模型的拟合程度,拟合数据越好偏差越低;而方差反应预测数据本身的离散程度。数据模型需要偏差小和方差也小,也就是需要模型聚焦在实际数据之中,预测数据既要准,也要聚,在实际当中这是很难调和的,只能选择一个折中平衡点,偏差与方差的关系如下图所示:

偏差与方差呈现的这种关系其实很好理解,为了使模型偏差低就自然需要更多点去拟合实际数据,而更多点必然会加剧数据离散情况,即方差变大。我们以射击运动员打靶为例感性的认识一下偏差与方差的关系:
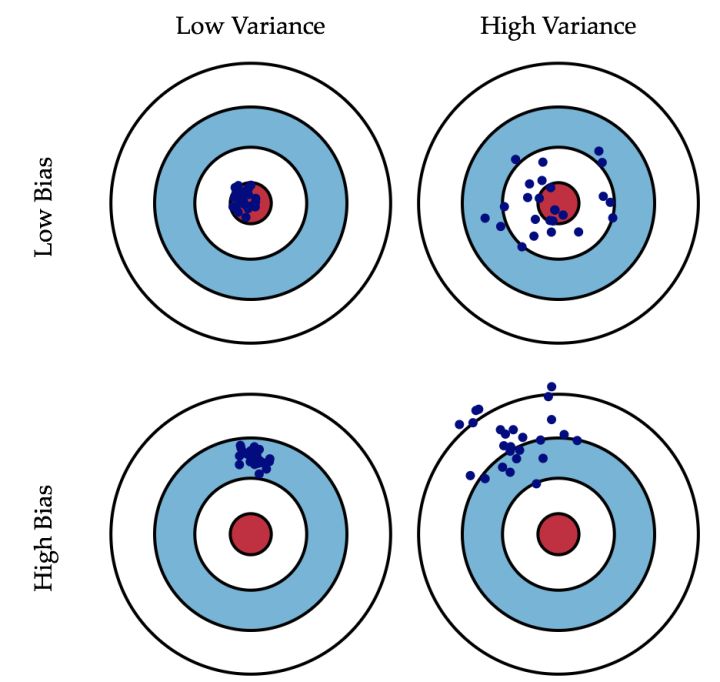
上面图表中左上图代表低偏差、低方差,可以看到射击点都命中红心,表示预测数据完美的契合实际数据;右上图代表低偏差、高方差,可以看到虽然数据也是均匀的分布与红心附近,但数据本身分的太开,表示预测数据过拟合。左下图代表高偏差、低方差,这样的效果看似很准、很聚集,但是中心点都不在红心上,发生了原则性的错误,这是欠拟合的表现,但是离散度比较低说'准心'其实还可以的,在实际应用中通过微调算法和参数就可以达到不错的效果;而右下图是高偏差、高方差,这时就不能用欠拟合来表述了,这种模型没有太大应用价值。
二、Baging算法
前面说了很多关于误差、偏差、方差的概念,这些概念对于理解和应用Bagging算法很有必要,现在说一下Bagging算法的过程。