SVM支持向量机详解
支持向量机(support vector machines, SVM)是二分类算法,所谓二分类即把具有多个特性(属性)的数据分为两类,目前主流机器学习算法中,神经网络等其他机器学习模型已经能很好完成二分类、多分类,学习和研究SVM,理解SVM背后丰富算法知识,对以后研究其他算法大有裨益;在实现SVM过程中,会综合利用之前介绍的一维搜索、KKT条件、惩罚函数等相关知识。本篇首先通过详解SVM原理,后介绍如何利用python从零实现SVM算法。
为便于理解,假设样本有两个属性,可以把属性值分别对应到二维空间轴的x,y轴上,如下图所示:
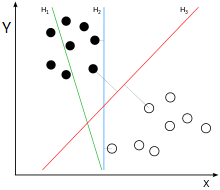
实例中样本明显的分为两类,黑色实心点不妨为类别一,空心圆点可命名为类别二,在实际应用中会把类别数值化,比如类别一用1表示,类别二用-1表示,称数值化后的类别为标签。每个类别分别对应于标签1、还是-1表示没有硬性规定,可以根据自己喜好即可,需要注意的是,由于SVM算法标签也会参与数学运算,这里不能把类别标签设为0。
还是对应于上图,如果能需要找到一条直线,将上述的实心点与空心点分为两个部分,当下次还有其他样本点时,将其属性值作为坐标绘制到坐标轴上后,根据新样本点与直线位置关系,就可以判断出其类别。满足这样直线有无数条,SVM是要找到最合适一条:观察上图,绿线肯定不行,该条分类直线在没有验证集前提下已经错了;而蓝色线和红色都可以实现分类,蓝色线与实心黑点靠的太近,相比而言,红色线更‘公允’些。红色线就是SVM需要找出的分类直线,数学语言描述红线的‘公允’特性可表述为:将黑点和空心点视为两个集合,如果找到一个直线,使得黑点集合中的一些点离直线最近,这些点到该直线距离为d;空心点集合中也能找到一系列的点,离直线最近,距离同样也是d,则该直线就是我们要找到线性分类器,同时称两个集合中离直线最近的点为支持向量,SVM支持向量机就是由此得名的。
一些算法书籍中这样描述SVM算法,找出一个直线,使得直线与两边集合最近的点的间隔空间最大,从上图也可以看出来,黑色点离蓝线最近的点,其距离小于到红线距离(直角的斜边)。能找到支持向量就一定找到分类直线,反之亦然,以上是针对两个属性值,通过观察二维平面即可以引出SVM的算法的特点,如果样本属性非常多呢,如何归纳算法的规律性?首先说下凸集可分离定理,该定理不仅是SVM的核心理论支持,更是机器学习算法的基石。
一、凸集可分离定理
还是以二维空间为例,中学时代我们就学过直线方程,比如有直线方程y=2x-1,如下图所示:
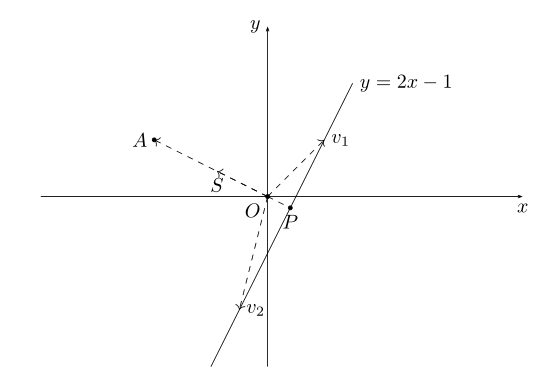
把直线方程y=2x-1写成内积形式:
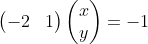
向量(-2,1)对应上图中OA向量,把OA向量变为单位向量,即方向与OA相同,模为1向量OS,S的坐标为 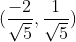 ,将直线方程两边同除以
,将直线方程两边同除以 ,可得:
,可得:
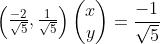
(x,y)代表直线y=2x-1上任意一点,上式说明y=2x-1上任意一点与单位向量S: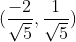 的内积是
的内积是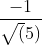 ,图中向量OP的长度为
,图中向量OP的长度为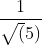 ,取负号是因为OP向量方向与OS方向相反;上图中向量v1、v2在OS向量上投影都是OP,这个例子说明:通过引入一个向量OS,直线y=2x-1上无数的点在向量OS上都可以用
,取负号是因为OP向量方向与OS方向相反;上图中向量v1、v2在OS向量上投影都是OP,这个例子说明:通过引入一个向量OS,直线y=2x-1上无数的点在向量OS上都可以用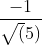 来表示,或者说,直线y=2x-1在向量OS上都可以用坐标(0,
来表示,或者说,直线y=2x-1在向量OS上都可以用坐标(0,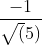 )表示。通过内积投影的方式,可以把高维数据变为向量上一个实数,这是一个线性泛函的过程,数学领域中常用内积来降低数据维度,把多维数据处理成一个实数便于后期分析、处理。
)表示。通过内积投影的方式,可以把高维数据变为向量上一个实数,这是一个线性泛函的过程,数学领域中常用内积来降低数据维度,把多维数据处理成一个实数便于后期分析、处理。
引申到任意维度时,上面方程可用集合公式表达:S:{x | pTx=α} x∈Rn。对应于上图:p向量对应向量OS,x为直线上任意一点,在SVM算法中,称x点构成的集合S为超平面。有时高维数据集合投影到向量p的内积值是一个范围:比如{x | pTx>=α}或{y | pTy<=-α},高维数据被投影到向量p的两个区间上:
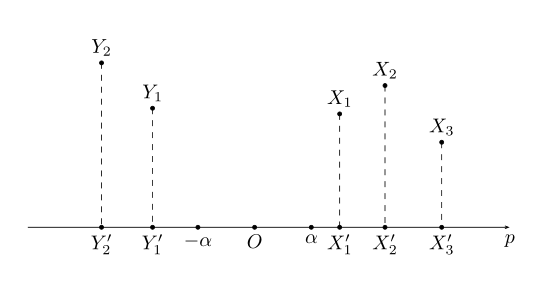
接下来介绍凸集分离定理:
上图中X,Y在高维空间中都是凸集,且X∩Y=Φ;将X、Y投影到向量p上后,可以得到两个凸集X',Y',在向量p上X'、Y'一定处在向量p的两端,即X',Y'两个凸集是可分离的。
注意定理中有两个条件,一是X,Y是凸集,二是X,Y交集为空集。X',Y'可分离意味着在向量p上可以将两者区分开,而X与X'、Y与Y'都是一一映射,X',Y'可区分开就间接地意味着X,Y也可区分开,这里所谓的'可区分开'也就是SVM所要实现的二分法。凸集可分离定理说明两个没有交集的凸集是线性可分的,同时,如果两个数据集不能线性分开时,可以通过核函数将数据变为两个凸集,所以凸集可分离定理对核函数生成也有着指导意义。
二、 SVM算法
2.1 超平面与最大间隔
前面介绍过,能把数据实现二分类的线性分类器称为超平面,SVM算法需要求出最大间隔的超平面,可设超平面为S:{x|pTx=α},由于pTx=α等式两边可除以一个正数就可以把p归一化为单位向量,不妨设p是一个已经处理后的单位向量,此设定不影响SVM算法。一般文献中,超平面通常写成隐函数形式:
S:{x|pTx-α=0} x∈Rn,p∈Rn,||p||=1
由几何知识可知,空间任意一点x到超平面S的距离公式为:
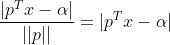
属于两个分类的支持向量到该超平面的距离都为d , d>0,由于支持向量是各自分类数据中,距离超平面最近的点,针对所有数据有以下不等式:
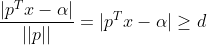 ⑴
⑴
公式(1)两边同除以d,可得: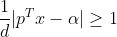 ,使用换元法,令:
,使用换元法,令:
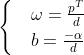 ⑵
⑵
这样就得到约束条件常见形式:
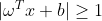 ⑶
⑶
接下来要把公式(3)脱掉绝对值符号,SVM是一个二分类问题:可设定ωTx+b>=1时分类标签y=1;ωTx+b<=-1时分类标签y=-1,这样一来,所有的数据都有不等式:
y(ωTx+b)>=1 ④
再回过头来看换元设定,ω=pT/d,等式两边取范数运算有:||ω||=||pT||/d=1/d,可得d=1/||ω||,SVM算法需要在满足公式4约束的基础上,使得间隔距离d最大。假设待分类数据共有m个,实现SVM算法等同于求解一个带有不等式约束的非线性规划问题:
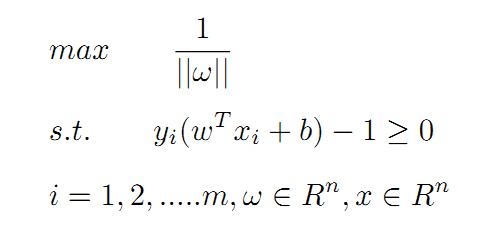
上面的问题也可以表述为求最小值的问题:
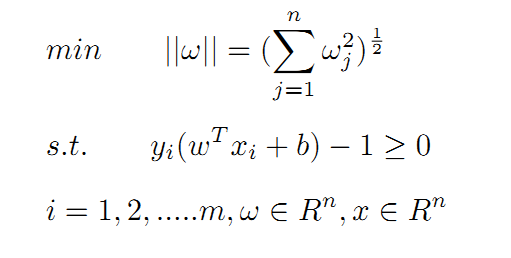 ⑤
⑤
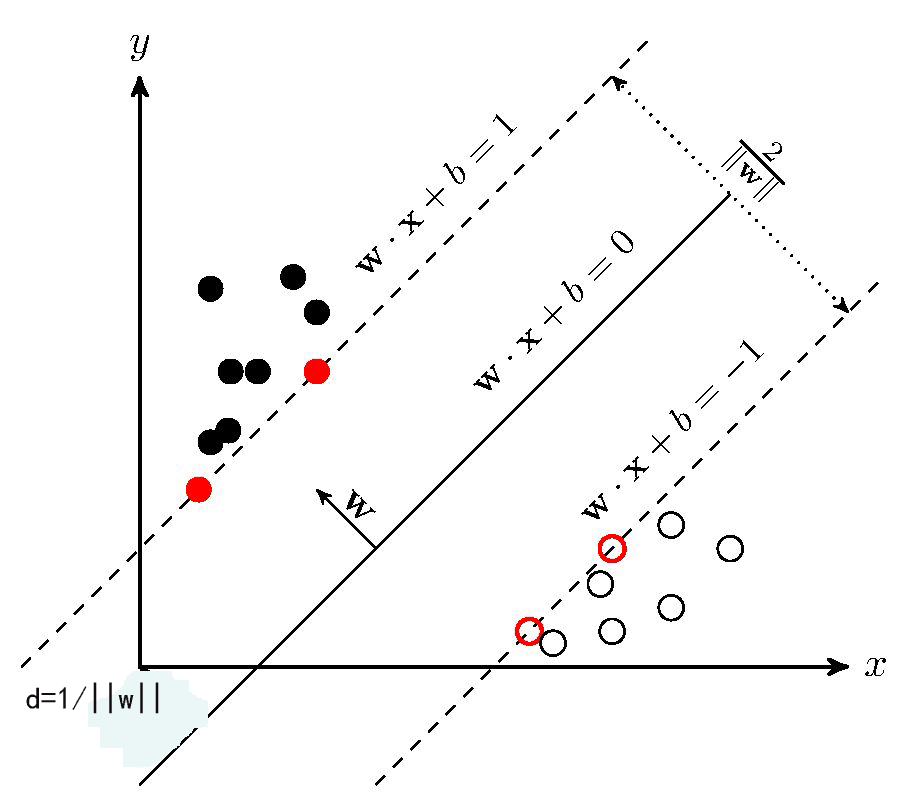
超平面实现分类效果、以及各个参数之间关系可参考下图:
2.2 最大软间隔
实践中由于异常数据的存在,导致超平面不能完全将数据分为两部分,如下图:
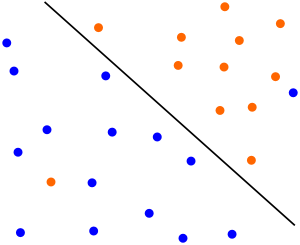
两个分类中混杂了少量的异常数据,除去极少数的异常点,上图中超平面能分离大多数样本。⑤式引入松弛变量后可以兼容上图的情形:
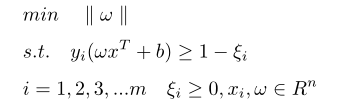 (5.1)
(5.1)
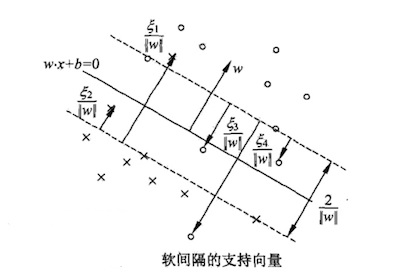
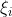 正常情况下等于0,表示样本点分列在支持向量的两侧;
正常情况下等于0,表示样本点分列在支持向量的两侧;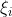 >0时代表的是异常数据:当0<
>0时代表的是异常数据:当0<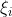 <1时,代表数据在超平面与支持向量之间,如上图中的点2和点4;而
<1时,代表数据在超平面与支持向量之间,如上图中的点2和点4;而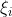 >1时代表数据到了对方空间中,如上图的点1和点3。满足(5.1)式的间隔称为软间隔,软间隔优化结果不仅需要支持向量的间隔最大,还要使得各个
>1时代表数据到了对方空间中,如上图的点1和点3。满足(5.1)式的间隔称为软间隔,软间隔优化结果不仅需要支持向量的间隔最大,还要使得各个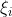 尽量的小。换句话说,超平面确定后,被定义为异常数据的样本个数要尽量的少。
尽量的小。换句话说,超平面确定后,被定义为异常数据的样本个数要尽量的少。
三、求解带约束的非线性规划问题
SVM算法最后归结为求解式(5),这是一个有约束的非线性规划问题,接下来通过两种方法求解,一种方案是利用之前介绍惩罚函数,优点是简单直接容易理解,不受约束条件数量的限制;另一种方案是数学解析法,其原理是拉格朗日对偶原理的应用,计算中涉及到对偶问题、鞍点、SMO算法等,解析法是一种理论性较强方法。
3.1 拉格朗日对偶
3.1.1 对偶问题
为后期求导方便,将公式(5)的目标函数f(ω)改为:
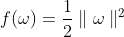
乘以一个正数后与之前优化问题是等效的,新的目标函数与约束条件合成一个函数L(ω,b,α):
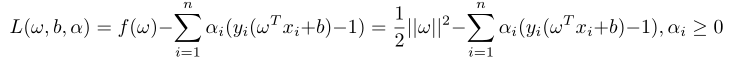
L(ω,b,α)称为拉格朗日函数,由于yi(ωTxi+b)-1>=0,αi≥0,在可行区内恒有L(ω,b,α)<=f(ω),如有常数ω*,b*,α*满足下面关系:
L(ω*,b*,α)<=L(ω*,b*,α*)<=L(ω,b,α*) ⑥
称ω*,b*,α*是L(ω,b,α)函数的鞍点,此时ω*,b*是原问题的最优解。观察⑥式,L(ω*,b*,α)是仅含有参数α的函数,产生这个函数的过程是:ω,b分别取不同的值,代入L(ω,b,α)后得到一系列参数为α的函数簇Φ,当ω=ω*,b=b*时,函数L(ω*,b*,α)是函数簇Φ中下界函数,图像上看,L(ω*,b*,α)在函数簇Φ所有函数的下方,L(ω*,b*,α)函数可用θ(α)=inf{L(ω,b,α)}表示,inf意为取得函数簇Φ的下界,当α=α*时,函数θ(α)有最大值,即L(ω*,b*,α)<=L(ω*,b*,α*);而α取不同值代入L(ω,b)后得到一系列参数为ω,b的函数簇Ψ,L(ω,b,α*)代表函数簇Ψ的上界函数,公式表示:φ(ω,b)=L(ω,b,α*)=sup{L(α)},当ω=ω*,b=b*时φ(ω,b)有最小值L(ω*,b*,α*)。
⑥式不等式形式称为弱对偶条件,当取等号时,L(ω*,b*,α*)是θ(α)函数最大值,同时也是φ(ω,b)函数最小值,此时为强对偶条件。SVM默认是满足强对偶条件的,满足强对偶条件时,max{θ(α)}=L(ω*,b*,α*)=min{f(ω)} ,也称下面的⑦与⑤是拉格朗日对偶问题:
max : θ(α)=inf{L(ω,b,α)}
s.t. α>=0 ⑦
上面过程没有给出鞍点就是K-T点证明、强对偶成立的条件,可参考相关资料详细研究,拉格朗日函数鞍点示意图如下:
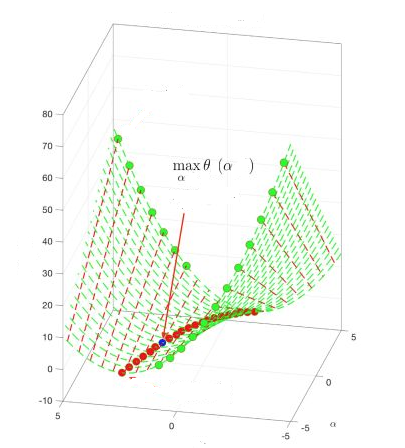
上图中红色虚线代表ω,b分别取不同的值,代入L(ω,b,α)后得到一系列参数为α的函数簇Φ,绿色点代表函数簇Φ中每个函数最大值;绿色虚线为α取不同值代入L(ω,b,α)后得到一系列参数为ω,b的函数簇Ψ,红色点代表函数簇Ψ中每个函数最小值。显然函数簇Φ中下界函数θ(α)的最大值、函数簇Ψ上界函数φ(ω,b)的最小值,两点重合,该点为拉格朗日鞍点。
求⑦最大值时首选要知道函数θ(α)的具体形式,已经知道,θ(α)是函数簇Φ的下界函数,函数簇Φ是把L(ω,b,α)中α视为符号常量、ω,b视为变量,那么求L(ω,b)最小值时,求导等于0时,ω,b都将是α函数,将ω,b代入L(ω,b,α)中即可得到θ(α)。
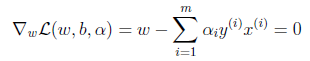
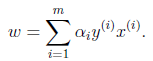 (7.1)
(7.1)
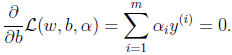 (7.2)
(7.2)
(7.1)代入拉格朗日函数L(ω,b,α)可得:
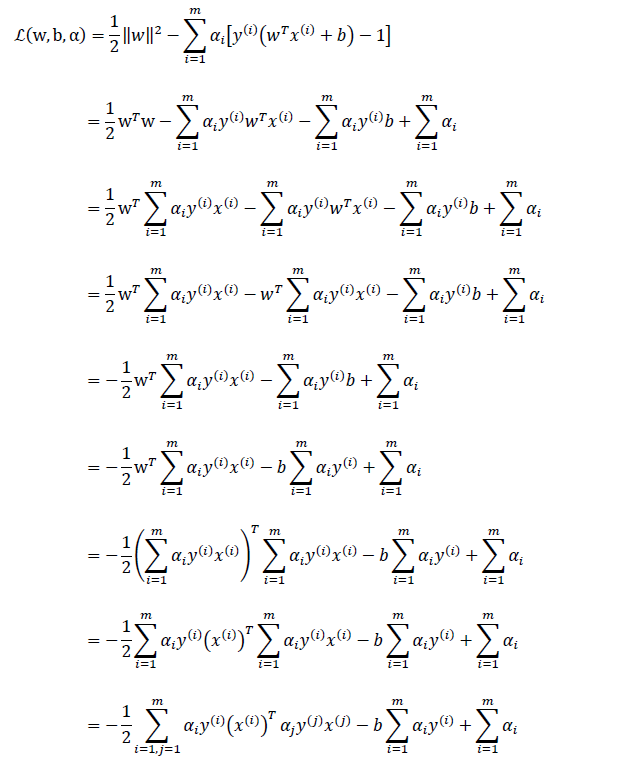
由于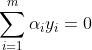 ,所以上式可化为:
,所以上式可化为:
θ(α)=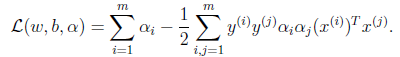 ⑧
⑧
求 max:θ(α)即可得到SVM的最优解,⑧是一个二次凸优化问题,求解⑧通用办法是利用SMO算法。
3.1.2 SMO算法
介绍SMO算法之前,先结合软间隔定义(5.1)式看看参数αi除了满足(7.1)、(7.2)还有其他哪些特性。软间隔要求间隔最大基础上,松弛变量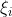 总体要小,即得到超平面之后,被定义为异常数据样本数量要尽量的少。按照这个定义生成新的拉格朗日函数:
总体要小,即得到超平面之后,被定义为异常数据样本数量要尽量的少。按照这个定义生成新的拉格朗日函数:
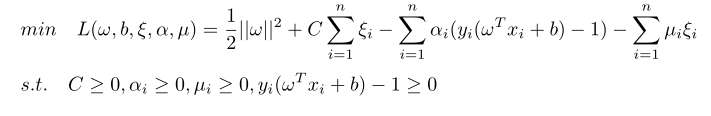 (8.1)
(8.1)
求解上式最小值的过程中,逐渐增大C将使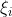 值变小,C是惩罚系数。按照对偶函数思想,为得到下界函数θ(α),先对其他参数求偏导得到以下等式组:
值变小,C是惩罚系数。按照对偶函数思想,为得到下界函数θ(α),先对其他参数求偏导得到以下等式组:
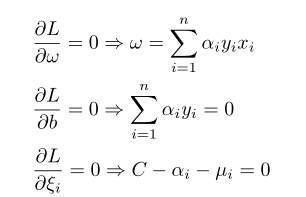
条件前两个结果之前已经推导过,最后一个条件说明0≤αi≤C。
SMO算法用坐标上升法来实现参数优化,该方法在之前文章中介绍过,详细可参考链接:梯度下降法。简略回顾下,坐标上升法选择一个参数vi同时固定并初始化其他变量,目标函数此时变为vi的函数,求导并置零后,vi变为其他固定变量的函数,代入初始值后,得到vi优化值,再切换到下一个变量,重复以上操作直至函数值收敛,得到最优解。
由于有条件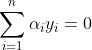 存在,若选择αi以外的变量固定,αi一定是个常量,所以SMO算法通常一次取两个变量后固定其余的变量。不妨设先取α1 、α2(注意,下标1和2不代表第一个样本和第二个样本),此时其他变量被初始化而固定,得到以下等式:
存在,若选择αi以外的变量固定,αi一定是个常量,所以SMO算法通常一次取两个变量后固定其余的变量。不妨设先取α1 、α2(注意,下标1和2不代表第一个样本和第二个样本),此时其他变量被初始化而固定,得到以下等式:
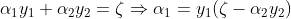 ⑨
⑨
上式中ζ是一个常数,上式代入到⑧式中,目标函数θ(α)变为只含有α2的函数:

K(xi,xj)代表利用核函数求两个样本向量的泛函,本篇中K是个内积函数,求θ(α2)的梯度:
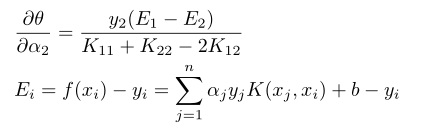
在α2初始值基础上,沿着梯度方向前进是最大值方向,这样就得到α2新的值:
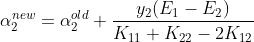 ⑩
⑩
得到α2新的值后接下来求α新的值:
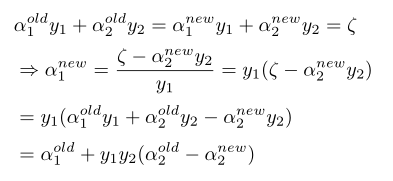 (10.1)
(10.1)
通过公式⑩得到α2新的值,实质是沿着梯度方向前进,且步长为1,如果读者了解一维搜索算法,能看出这里步长应该是计算出来的,不能盲目直接设置为1。步长系数的确定,在SMO算法中体现为对α1、α2新值的进一步裁剪。再回过头来看公式⑨,根据y1,y2是否同号,α1、α2会有以下两种线性关系:
y1≠y2时:α1-α2=k
y1=y2时:α1+α2=k
根据k为正负情况,以上两种线性关系可用下图表示:
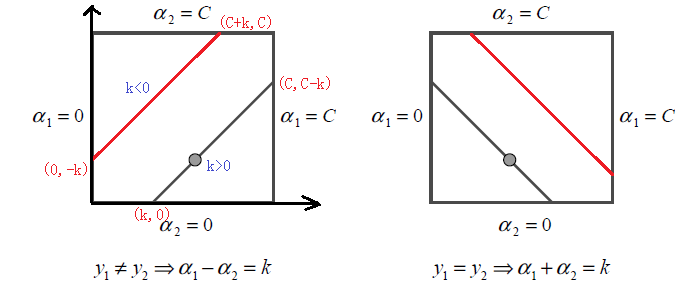
通过上图可以得到α1、α2上下界,显然当y1≠y2时:
下界: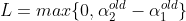
上界: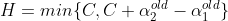
而当y1=y2时:
下界:
上界: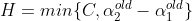
有了上下界后,即可对新值做剪裁,具体规则为:
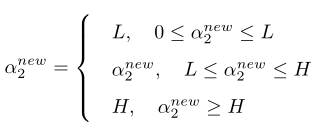
剪裁本质就是修改步长系数的过程,将剪裁后的α2新值代入公式(10.1)后获得α1新值。得到α1、α2后按照坐标上升法依次得到其他参数值,然后迭代多轮重复计算,可得到全体α值,同时根据公式(7.1),可得参数ω值。
最后看下如何更新参数b的值,根据条件C-αi-μi=0,αi的新值经剪裁后恒有约束0≤αi≤C,接下来根据αi值的范围分别讨论。优化问题(8.1)有最优解时应满足KKT条件,即有下面等式存在:
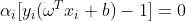
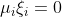 (11)
(11)
情形一、当αi=0时,可得μi>0,ξi=0,此时有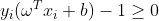 ,代表超平面可正确分类样本点xi,样本点xi在支持向量的两侧,大多数样本都是这种情形。
,代表超平面可正确分类样本点xi,样本点xi在支持向量的两侧,大多数样本都是这种情形。
情形二、当0<αi<C时,可得μi>0,ξi=0,根据公式(11)判断出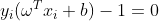 ,样本点xi此时是支持向量。
,样本点xi此时是支持向量。
情形三、当αi=C时,此时μi=0,ξi≥0并且有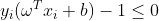 ,此时样本点xi大概率是一个异常点数据(是否是异常点还要看ξi值)。
,此时样本点xi大概率是一个异常点数据(是否是异常点还要看ξi值)。
对于情形二,由于αi对应的xi是支持向量,不失一般性,可设有0<α1<C:

对于情形一、情形二时,即α1、α2在边界时,这时两个变量的组合有三种:(0,0),(C,C),(0,C),通过观察α1、α2的线性关系图可以发现,在边界时,其实只有(0,C)这种情况。不妨设α1=0,α2=C,设b的目标值为bgoal,α1=0对应着x1是被正确分类的点,这时有:

而x1强行设为支持向量时,可利用公式(11.1)计算出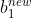 ,此时有
,此时有
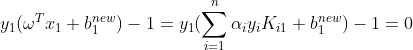
对比上式,显然有
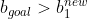
同样对于α2=C对应的样本点有:
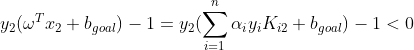
x2强行设为支持向量时,可利用公式(11.2)计算出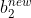 ,此时有:
,此时有:
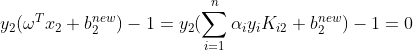
可以导出:
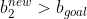
综上所述,对应情形一、情形二时,bgoal一定是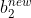 和
和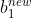 之间的某个值,或者说
之间的某个值,或者说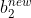 和
和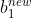 之间值都满足KKT条件,在这种场景下通常取b得值为两者平均数:
之间值都满足KKT条件,在这种场景下通常取b得值为两者平均数:
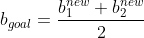
至此,就分析完SMO算法主要过程,下面代码利用SMO实现SVM分类功能: