最优化问题中常常需要求解目标函数的最大值或最小值，比如SVM支持向量机算法需要求解分类之间最短距离，神经网络中需要计算损失函数的最小值，分类树问题需要计算熵的最小或最大值等等。如果目标函数可求导常用梯度法，不能求导时一般选用模式搜索法。

一、梯度法求解最优问题

    由数学分析知识可以知道，函数在一个点的梯度方向是函数值增大的最快方向，与之相反，梯度的反方向是函数值变小的最快方向，函数值在定义域内可以用等值线形式来表示。假设求目标函数最小值，可在定义域内任选一点，求出该初始点梯度反方向，沿着这个反向得到新的一个点，再求出新点的梯度反方向，迭代若干次后，可通过计算函数值的误差范围结束迭代获得函数最小值。根据具体的应用，有的是需要计算函数最值，有的是需要求满足最值时的自变量（定义域的坐标），梯度法计算过程可以通过下图来理解：

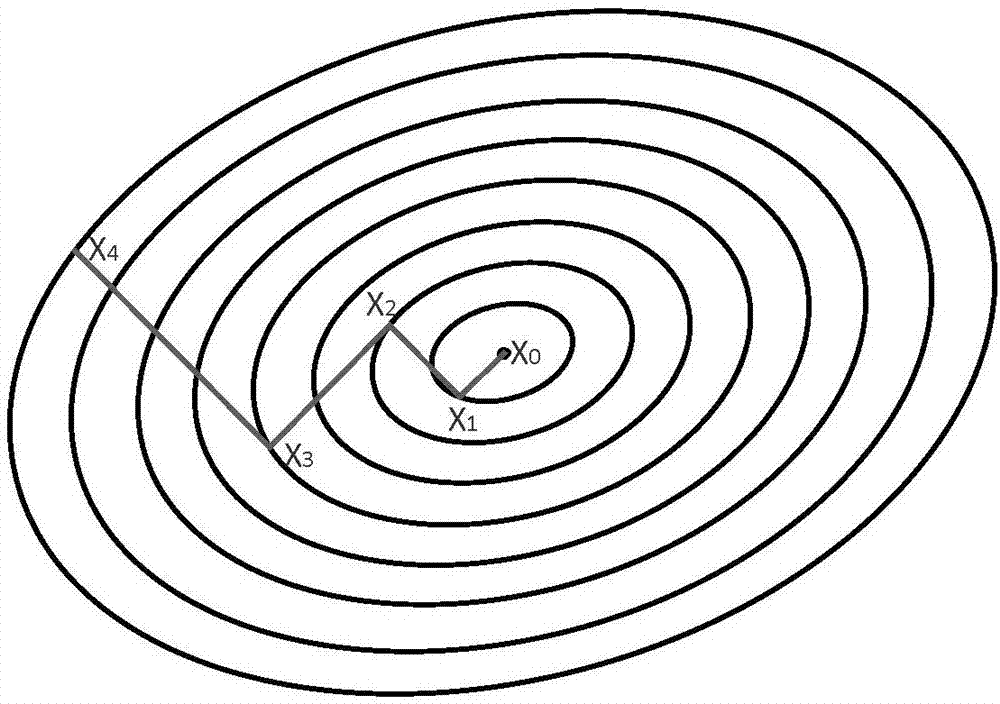
    这里需要强调一点，等值线上任选一点后，可沿着梯度下降方向无约束的移动，所以这里讨论的是无约束条件的最优化问题，无约束的问题处理起来还是比较简单的，有约束的问题需要另外的算法，如单纯形法、可行方向搜索等，也可以将有约束的问题变为无约束的问题，具体可参考惩罚函数一章。

    用一段代码介绍下梯度法求解最优化问题，本例是用最小二乘法求线性回归问题，如有一组样本数据x_i和y_i，假设y_i=ax_i＋b，即x_i和y_i存在线性对应关系，其中a,b是未知参数，需要从所给的样本中计算出a,b值。由最小二乘法知，要求出a,b的最优解实际上就是求平方误差函数的最小值，当得到最小值后其自变量值：a,b即为线性关系函数的参数，注意这里x_i、y_i是已知值来自于样本数据。

import numpy as np
import  math
import scipy
from sympy import Matrix
import scipy.linalg
class optclass(object):
    def __init__(self,  error):
        self.error = error
        self.direction=np.array([[1,0],[-1,0],[0,1],[0,-1]])

    #求一阶导数
    def P_firstderivative(self,step,theta1,theta2,  grad_theta1, grad_theta2 ,x,y):
        d1=0
        for i in range(y.shape[0]):
            d1=d1+((theta1-grad_theta1*step)*x[i]+theta2-grad_theta2*step-y[i])*(-grad_theta1*x[i]-grad_theta2)
        return d1

    # 求二阶导数
    def P_secondderivative(self,  grad_theta1, grad_theta2  ,x ,y):
        d2=0
        for i in range(y.shape[0]):
            d2=d2+ (-grad_theta1*x[i]-grad_theta2)**2
        return d2

    # 牛顿法实现一维搜索，获得步长
    def newton(self,theta1,theta2,  grad_theta1, grad_theta2 ,x,y_):
        stepx, l, iterNum = 0, 1e-4, 0
        dx_1 =self. P_firstderivative(stepx, theta1,theta2,  grad_theta1, grad_theta2 ,  x,y_)
        while abs(dx_1) > l:
            dx_1 = self.P_firstderivative(stepx, theta1, theta2, grad_theta1, grad_theta2, x, y_)
            dx_2 = self.P_secondderivative(grad_theta1, grad_theta2 ,x,y_)
            stepx = stepx - dx_1 / dx_2
            iterNum = iterNum + 1
        return stepx
        #计算误差
    def calerror(self,theta1,theta2,x,y):
        error=0
        for i in range(y_.shape[0]):
            error = error  + 0.5 * ((x[i] * theta1 + theta2 - y_[i]) ** 2)
        return error


    def gradiatdesc(self,y_,x,theta):
        grad_theta1,grad_theta2=0,0
        NITER=100000
        for t in range(NITER):
            for i in range(y_.shape[0]):
                grad_theta1 = grad_theta1 + (theta[0] * x[i] + theta[1] - y_[i]) * x[i]
                grad_theta2=grad_theta2+(theta[0]*x[i]+theta[1]- y_[i])
            distance=math.sqrt(grad_theta1**2+grad_theta2**2)
            grad_theta1=grad_theta1/distance
            grad_theta2 = grad_theta2 / distance
            #1.1 利用一维搜索获得最佳步长系数
            step=self.newton(theta[0],theta[1] ,grad_theta1,grad_theta2,x,y_)
            theta[0] = theta[0] - grad_theta1 * step
            theta[1] = theta[1] - grad_theta2 * step
            error=self.calerror(theta[0] ,theta[1] ,x,y_)
            #print('误差%0.3f 步长%0.2f'%(error,step))
            if(error<= self.error):
                break
            grad_theta1, grad_theta2 = 0, 0
        return  theta[0],theta[1]


if __name__=='__main__':
    theta1,theta2=2.4,8.21
    theta=np.array([0,0],dtype=np.float32)
    o=optclass(1e-5)
    x=np.linspace(1,20,100)
    y_=np.array([theta1*xx+theta2 for xx in x ])
    a,b=o.gradiatdesc(y_, x, theta)
    print('theta1=%0.3f theta2=%0.2f' % (theta1, theta2))

在梯度下降搜索最值过程中，为了防止每次步长太大而跳出极值点,在代码注释标记1.1处，

 step=self.newton(theta[0],theta[1] ,grad_theta1,grad_theta2,x,y_)

利用牛顿法一维搜索获得最佳步长系数，具体做法是：将参数

theta1=theta1-参数theta1梯度*步长

theta2=theta2-参数theta2梯度*步长

代入目标函数,此时目标函数变为只有步长系数的一元函数，求解该函数最小值即可获得在当前前进方向下最优的步长，关于一维搜索知识请看本站文章：一维搜索。

上面方法称为GD,所有样本都参与了运算，并用一维搜索计算出最佳步长，这样的优化结果是最好的，在实际应用中，当样本数量非常大时GD是非常耗时的，在训练模型时往往采取多轮计算，每轮计算随机抽取样本中一部分数据集参与运算，对参数进行逐步优化，称为SGD(随机梯度下降)。另外，对于小样本情况利用一维搜索是非常准确的，而有些模型如一些神经网络动辄上亿的参数，此时再用一维搜索以目前计算机即使超级计算机的算力也是无法达到的，在SGD基础上引入动量（momentum）后,诞生了Momentum、Adagrad、Adadelta、RMSprop、Adam等优化算法，这些算法都是利用不太复杂的计算，动态调整步长系数实现算法的逐步收敛，也算是在效率和准确率之间折中办法。 

二、模式搜索求解最优化问题

    2.1 模式搜索法介绍

    在实际应用中有时函数是不可求导的，甚至函数本身的形式都不知道，这时梯度法显然不再适用，模式搜索法就应运而生。模式搜索法是一种获得函数最值通用算法，当目标函数不可求导时其等值线还是存在的，只不过与可导函数相比，其等值线看上去不是那么'顺滑'。利用模式搜索法对目标函数只有一个要求'目标函数定义域是一个凸函数'，凸函数、凸集可以想象成一个既没有'洞'，也不会相互重叠的区域，这种类型函数的等值线不会相交，只有保证这点才能使用模式搜索法。

    模式搜索法思想与梯度法一样，都是寻找函数变大或变小的方向，如求解函数最大值问题，此时不能直接求出某一点的梯度时，可以退而求其次，找出一个与梯度方向大致相同的向量，沿着这个向量方向运动不断变化调整，'方向大致相同'用几何语言描述是：选择的方向与梯度方向夹角在0-90度之间。方向从线性空间的角度来说是一个向量，由于线性空间中任何一个向量都可以用基线性表示，等值线所在的定义域是一个线性完备空间，可以用线性空间的基表示函数变化的方向，以求函数最小值为例，模式搜索法算法可以这样表述:

(1) 设初始点为x₁,等值线所在线性空间有e₁,e₂,...e_n个基，初始步长为s，方向系数α>=1,缩短因子β∈（0,1）,误差ε,并设y₁=x₁,k=1,j=1 。

(2) 计算f(y_j+e_j*s),如果f(y_j+e_j*s)<f(y_j),则设：

y_j+1=y_j+e_j*s  

转到步骤4；如f(y_j+e_j*s)≧f(y_j)转到步骤3。

(3) 如f(y_j-e_j*s)<f(y_j),则设：

y_j+1=y_j-e_j*s ；否则，则令

y_j+1=y_j,即回到开始尝试e_j时的起点_，转至步骤4。

(4) 这一步主要是切换到下一个基方向，如果j<n,则置j=j+1,转到步骤2；否则转到步骤5。

(5) 到这步意味着已经遍历所有基的方向、包括其反方向，如果f(y_n+1)<f(x_k),则转到步骤6；否则转到步骤7。

(6) 到这步代表遍历所有基方向后，且新的点函数值小于起始点的函数值，但函数值还有变小的空间。此时令x_k+1=y_n+1,并设

y1=x_k+1+α(x_k+1-x_k),k=k+1,j=1,转到步骤（2）。

(7) 如果步长s≦ε，退出计算，得到最值点；否则,设：

s=s*β , y₁=x_k , x_k+1=x_k

k=k+1, j=1,转到步骤2。

模式搜索步骤还是挺繁琐的，可以归纳一下，模式搜索沿着一个基方向寻找函数值变小的方向，如果该方向函数值没有降低，则沿着基的反方向寻找，如果都没找到则切换到下一个基，依此循环，如果所有的基方向都找不到，则回到原点，缩短步长，重新开始搜索。可见这种方法要把基方向都遍历一遍，全部遍历后，转入上面步骤5，此时检查：如果最后找到点y_n+1小于开始点函数值，则y_n+1出发，沿着开始点x_k指向y_n+1方向再前进α步长，得到新的搜索起始点，这段描述参考下图：

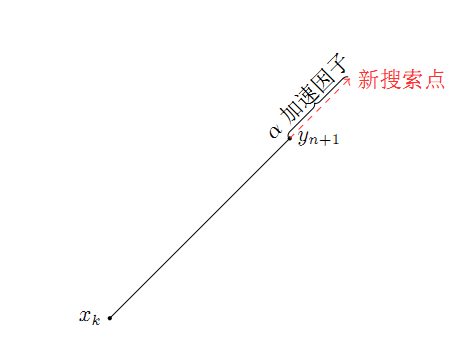
    x_k是初始点，通过遍历所有基方向找到点y_n+1后，并不是单纯将y_n+1作为新的搜索起始点_，算法中中有一个经验内涵：既然千辛万苦找到了y_n+1，那么沿着找到方向再前进一点应该也是满足条件的，算法中会沿着该方向再前进α长，有时α也称为加速因子。在实际开发中，将该α值适当调高一些，有时会以百倍的效率缩短算法过程。

    模式搜索与梯度法都是在函数等值线上搜索，两者区别参考下图：

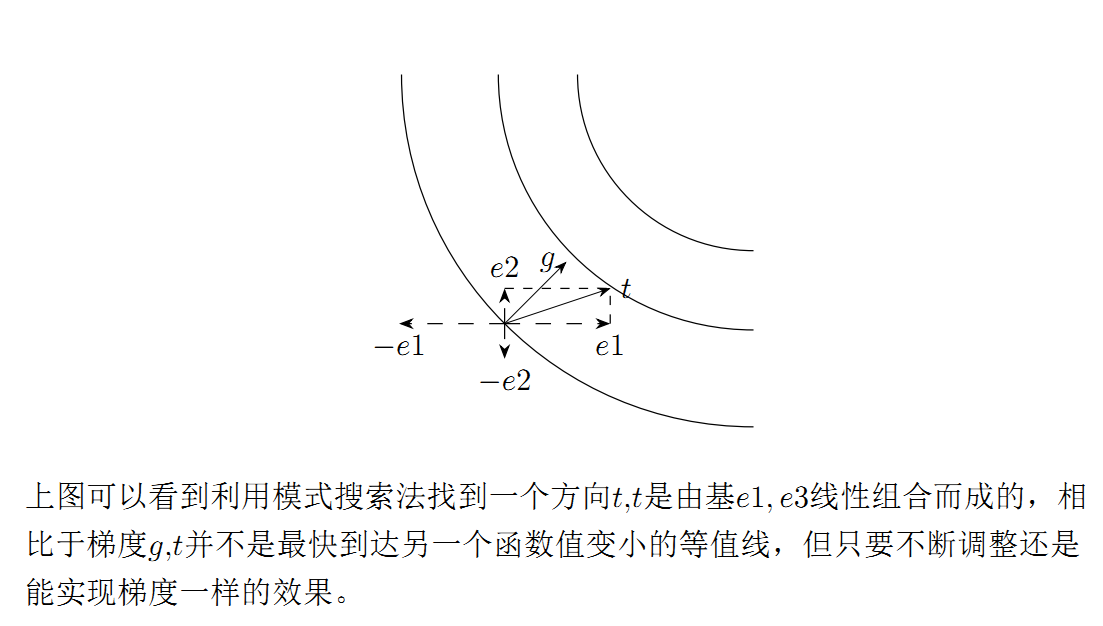
可以看出模式搜索法像极了一个左顾右盼的人，站在十字路口每个方向都尝试一下，试图找到函数的最值的方向；如果目标函数是凸集函数，最终还是可以到达目的地，上述算法描述很复杂，但幸好用编程实现并不难。

2.2 代码说明

下面的代码是利用模式搜索法实现之前线性回归问题，实现核心代码为modesearch函数，可根据注释参考：