pca全称是Principle component analysis，译为主成分分析，比如描述一个人信息时会用体重、身高、发型、爱好、收入、职业等信息，有时根据一个人的体重、身高、发型基本可以确定其性别，例如说一个女孩子是假小子，可能这个女孩有一个板寸头、身材很高，从众多属性中选取一两个，而无需其他属性作为参考就确定了一个分类，pca就是这样一个处理数据常用手段，即利用较少的属性对一组数据分类，pca是一个降维的数据处理手段,现实中的数据在计算机中可以用一个m行n列矩阵表示，n列可以是体重、身高、发型、爱好、收入、职业等属性信息，每一行就代表一个具体人。利用pca降维的过程是利用线性代数处理数据的过程，先介绍与PCA有关的线性代数知识。

一、基变换（坐标变换）

    以二维数据为例，平面直角坐标系有一个数据是(2,1)，代表x轴坐标是2，y轴坐标是1。在线性代数里，平面直角坐标系描述的是一个二维空间，x轴和y轴代表两个基。事实上，二维空间里可以有无数个基，常用的两个基是：x轴（0,1）T ，y轴（1,0）T,看下切换不同基效果图：

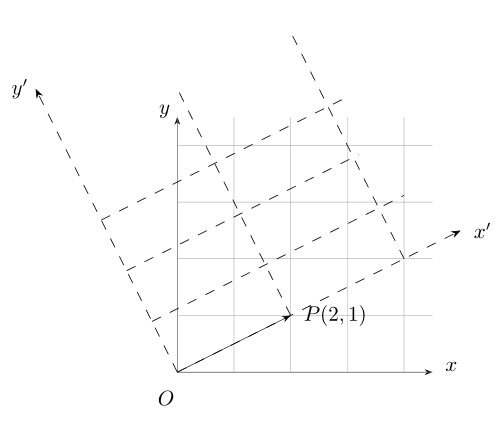
基变换利用线性空间不同基表示同一个向量时，向量本身没有发生变化，变化的只是向量在不同基下坐标值。基变换实现降维后原坐标向量变为稀疏向量，即大部分坐标值变为0，而坐标向量非零部分所对应的基为数据的主要特征部分，基变换的目的就是要找到满足以上条件的基，线性空间不同基之间可以相互转化，接下来介绍过渡矩阵的概念。

二、线性映射与线性变换

      将一个Rm向量映射成一个Rn向量则称为一个线性映射，比如将一个三维向量(2,1,3)映射成二维向量(2,1),也可以维度变大,如映射成(2,1,3,10），如果线性映射后的向量维度和原来一样即Rm映射成Rm，这种线性映射称为线性变换。可以将线性映射理解为函数，那么两者之间很多概念是对应的，比如m维线性空间有m个基，通过线性映射将这m个基映射为一个n维空间，新生成的n维空间相当于函数中值域。

    线性变换和基变换都在一个空间里将一个向量映射成另一个向量，所不同的是，基变换映射的向量与原向量是一一映射（单射、满射），并且是恒等映射，即前后表示的是一个向量；线性变换则不同，例如将一个三维坐标（1,2,3）通过线性变换变成了（1,2,0）即将z轴坐标变为0，这代表将任意三维向量投影到xoy平面，相应的（1,2,3),(1,2,4),(1,2,5）等等都可以变换为（1,2,0），这就导致三维空间产生向量之间多对一映射关系。线性变换的过程也可以用一个矩阵来描述，该矩阵叫做线性变换的矩阵表示。

当矩阵表示是满秩时，就能产生一一映射的效果；而矩阵表示不是满秩即为奇异矩阵时，产生的是多对一映射效果。这是因为线性变换后的值域的维度加上零空间的维度等于原来空间的维度，只有矩阵表示满秩时，线性变换T的零空间的维度是0（A满秩时，方程Ax=0的解只有全部是0），此时线性变换值域的维度才等于原来的维度。 

     基变换可以理解为测量一个1cm的物体，用带有厘米尺子测量时，显示的刻度是1，而用英寸的尺子测量时刻度是0.39（一厘米=0.39英寸），尺子刻度对应同一个物体在不同坐标系的坐标值，坐标系、基（更换不同单位的尺子）发生变化后，物体本身没有发生变化。线性变换变换更像一个熟练工人的机床，既有很多不同单位尺子（可以实现基变换的效果），也可以加工零件使零件使之可大可小。

观察(2.1)式，线性空间基变化时坐标向量也同时变化，基与坐标同时变化就确保了基变换前后表示的是同一个向量，再来看经过线性变换后向量坐标的变化，通过下面叙述，可以一次线性变换近似包含了两次基变换的过程。

(2.3)中线性变换后基也可以像基变换一样用(T(α1),T(α2),T(α3),...,T(αn))=(β1,β1,β3,..βn)表示，与公式(2.1)不同的是，线性变换后坐标没有变化，依然是变换前坐标(x1,x2,x3,..xn)。之前说过，基变换时坐标同时变化，确保了前后都是同一个向量，而线性变换后的向量还是沿用之前坐标，这就导致线性变换实际上产生了一个新的向量；另外一点，当线性变换的矩阵表示A不是满秩时，T(α1),T(α2),T(α3),...,T(αn)一定有0向量，这就是先前叙述的‘线性变换后的值域的维度加上零空间的维度等于原来空间的维度’，而基变换中所有的基都是线性不相关的非零向量。

    (2.3)式新生成的向量可用w来表示，w在线性空间V中，所以w也可以用原来的基α1，α2，α3，...，αn表示。

可以看出，线性变换包含了两次换基的过程:第一次基变为(T(α1),T(α2),T(α3),...,T(αn)),原向量变为新的向量w;第二次再回到基α1，α2，α3，...，αn下，并把向量w用基α1，α2，α3，...，αn线性表示，第二次是基变换过程。由于线性变换最后一步是回到原来基下，所以线性变换的从结果来看是在原线性空间中，将一个向量变换为另一个向量。基变换、线性变换也可以这样归纳：基变换是向量不动，坐标系发生变化；而线性变换是坐标系不动（其实是动了2次，结果又回到原来坐标系下），向量发生了变化。

三、pca算法原理

    pca算法使用了用基变换，需要补充一点，本例中基变换的过渡矩阵P是酉矩阵，而酉矩阵是一个可逆矩阵、标准正交矩阵，同时有性质PT=P-1,将这个等式两边取转置，还可以得到酉矩阵具有下面性质:

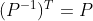     (3)

  接下来结合一段python代码来展示pca的算法过程，选取例子是熟悉的鸢尾花数据。这组鸢尾花数据可以分为三类，分别是山鸢尾 ，北美鸢尾，变色鸢尾，而鸢尾花具有4个属性，分别是花萼的长度、花萼的宽度、花瓣的长度，花瓣的宽度，算法展示的是利用其中两个属性即完成分类的过程，具体代码如下：

import numpy as np
import  math
from sklearn.datasets import  load_iris
from sklearn.preprocessing import  scale
import  scipy
import  matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
data=load_iris()
specimen=data['data']
target=data['target']
specimen_scale=scale(specimen,with_mean=True,with_std=True,axis=0)#1.1
specimen_corr=np.corrcoef(specimen_scale.T)#1.2
eig_val,eig_vec=scipy.linalg.eig(specimen_corr) #1.3
P=eig_vec#1.4 过渡矩阵
#P是酉矩阵 P的逆等于P的转置矩阵
#下面代码可以直接写成specimen_new_cor=np.dot(  specimen_scale, P)
specimen_new_cor=np.dot(  specimen_scale, np.linalg.inv(P).T )#1.5
plt.figure(1)
plt.scatter(specimen_new_cor[...,0],specimen_new_cor[...,1],c=target )
plt.xlabel("主成分一")
plt.ylabel("主成分二")
plt.show()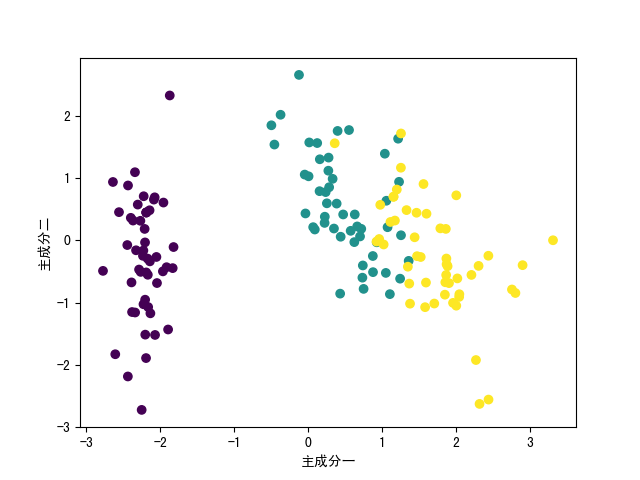

三个不同颜色代表不同鸢尾花类别，上图说明使用两个成分就可以较为清晰的将数据分成3类，接下来就几个关键点说明一下。

(注释为1.1)：实现量纲统一

specimen_scale=scale(specimen,with_mean=True,with_std=True,axis=0) 这句代码的意思是将每一列数据，即所有来自同一个属性的数据做量纲上统一，具体办法是每个数字减去平均数后除以方差。

(注释为1.2,1.3)：利用特征向量分解找出数据最大变化的方向，即发现四个新的基。