CNNs-卷积神经网络
卷积神经网络(Convolutional Neural Networks, CNN)是应用最多、研究最广的一种神经网络,卷积神经网络(以下简称CNN)主要用于图片分类,自动标注以及产品推荐系统中。以CNN实现图片分类为例,图像经过多个卷积层、池化层复合而成的组件后,实现图像降维并提取到主要特征,最后再利用全连接神经网络实现分类,一个完整CNN实现识别图像的示意图如下:
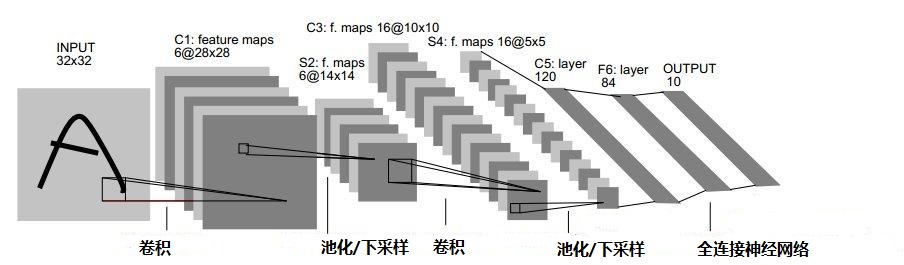
将一个矩阵用其中元素最大值或平均值代替称为下采样,在CNN中称为数据池化,池化可以有效地实现数据降维;相反从池化后结果再将数据还原称为上采样,CNN实现反向传播时需要先上采样后求参数梯度。CNN的核心是卷积运算,卷积操作可以提取图像不同的特征,当然一个图像的特征有很多,模型后端的全连接神经网络往往以交叉熵作为损失函数,通过交叉熵反馈过来信息,CNN可以调整卷积参数,找到最适合分类的特征数据。
一、卷积神经网络前向传播
1.1 卷积层
卷积常用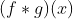 表示,根据数据连续与否型分为积分和离散两种形式,积分形式:
表示,根据数据连续与否型分为积分和离散两种形式,积分形式:
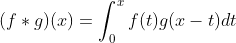 ①
①
离散形式:
 ②
②
公式①和②很难对卷积有一个感性的认识,通常介绍卷积时都会以信号处理为例,如下图f(t)是一串输入信号,自变量t代表时间,g(t)称之为系统响应,下图中g(t)代表信号的随时间衰减过程,信号在t=0时信号在t=20后大小为f(0)*g(20),而t=20时信号输出为f(20)*g(0),显然在t=20时,t=0的信号已经衰减的差不多了。
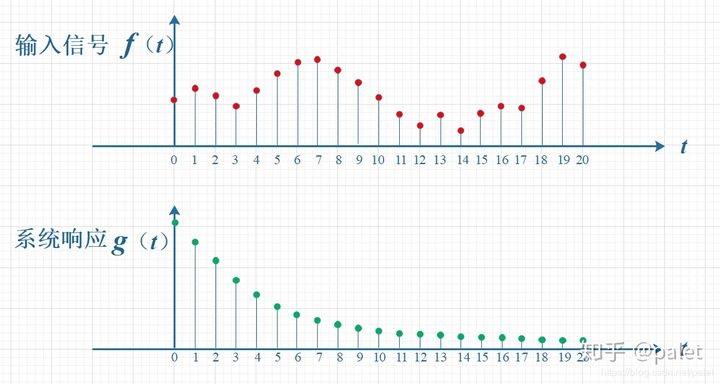
如果想知道任意一个时刻信号的输出,比如t=10时,信号输出是t=0,1,2,3...10各个输入信号f(t)与g(t)作用汇总后的一个数值,输出信号out可表示为:
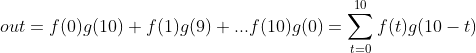
上式对应公式②,即离散形式的卷积公式,上式计算过程可用下图来表示:
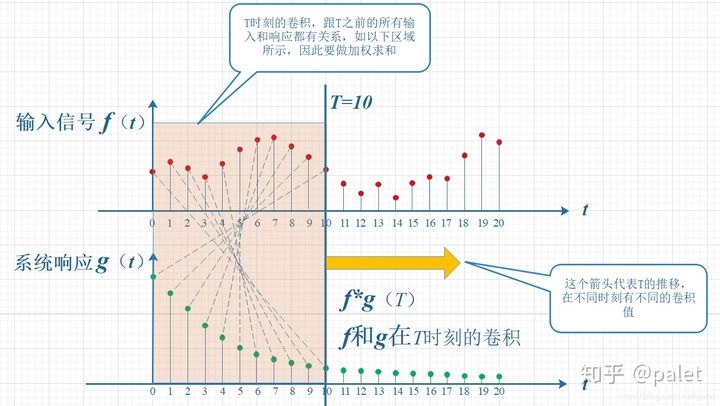
上图中变量间对应关系有些扭曲,更多时候上图也转化为下图更为形象:
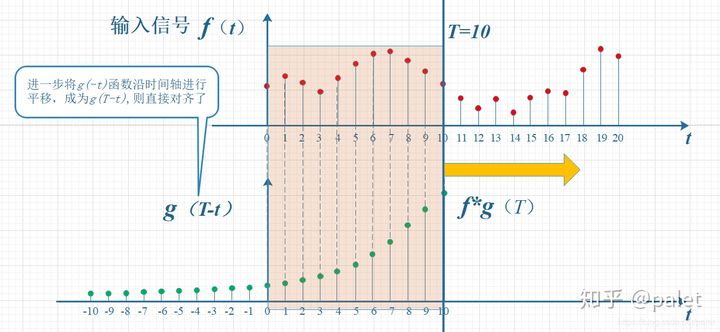
利用卷积运算CNN可实现数据降维:上面的例子中输入信号f(t)是一个向量,通过卷积运算汇总变为一个常量,当输入信号改变,系统响应函数g(t)不变时,不同信号与g(t)卷积后都变成为一个实数,以上图为例,在T=10时可以想象有一面墙,不同输入信号卷积后映射在T=10墙体的不同高度上。
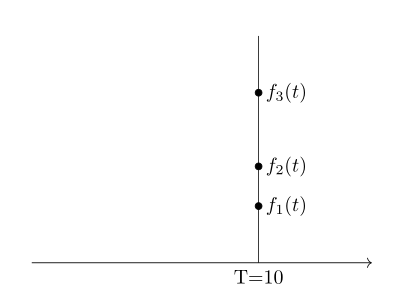
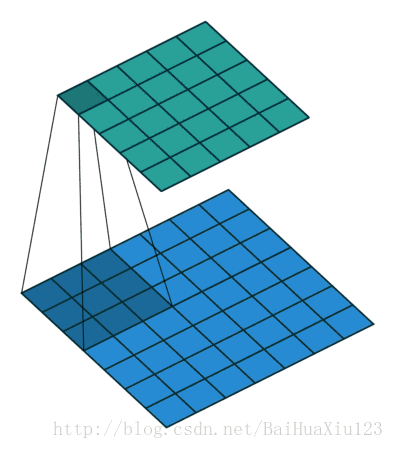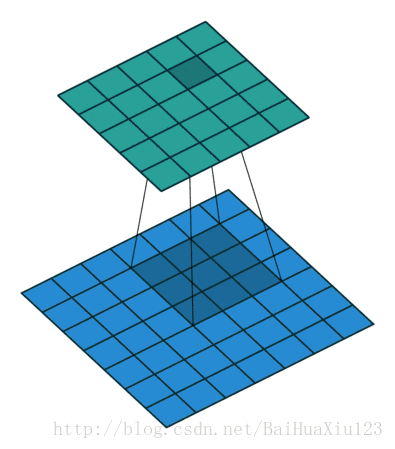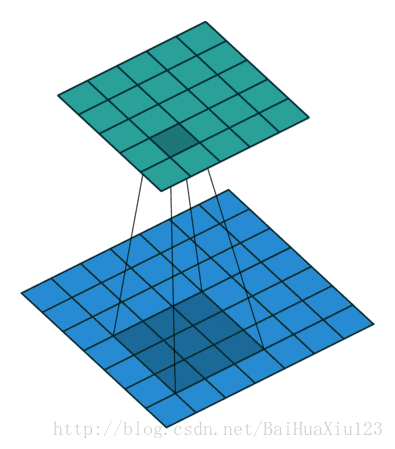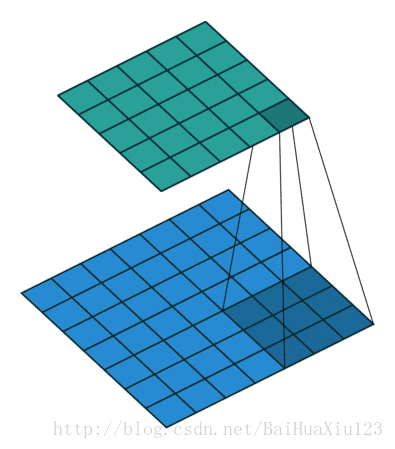
不同高度代表不同输入信号在g(t)下有不同的特性,通过卷积实现了信号的特性分离。在人工智能算法中常将复杂的数据处理成单一的实数,比如利用范数可以把矩阵变为一个实数,利用内积把两个向量距离变为一个实数,泛函分析中将求一个线性算子范数等。CNN处理图像时,上述的信号f(t)可引申为二维像素值,g(t)在CNN中称为卷积核,典型的卷积操作如下图所示:

下图是一个卷积的动态过程:
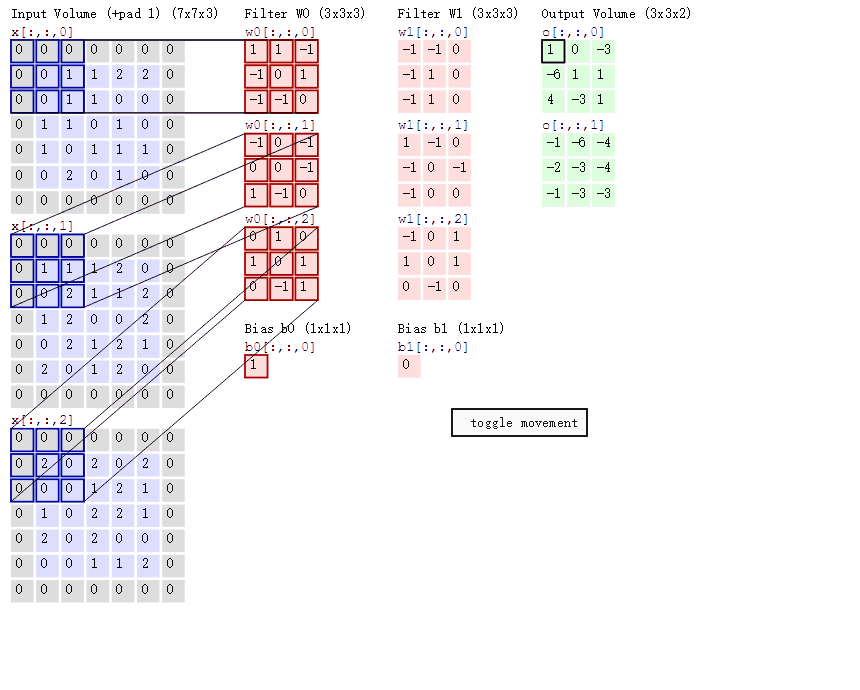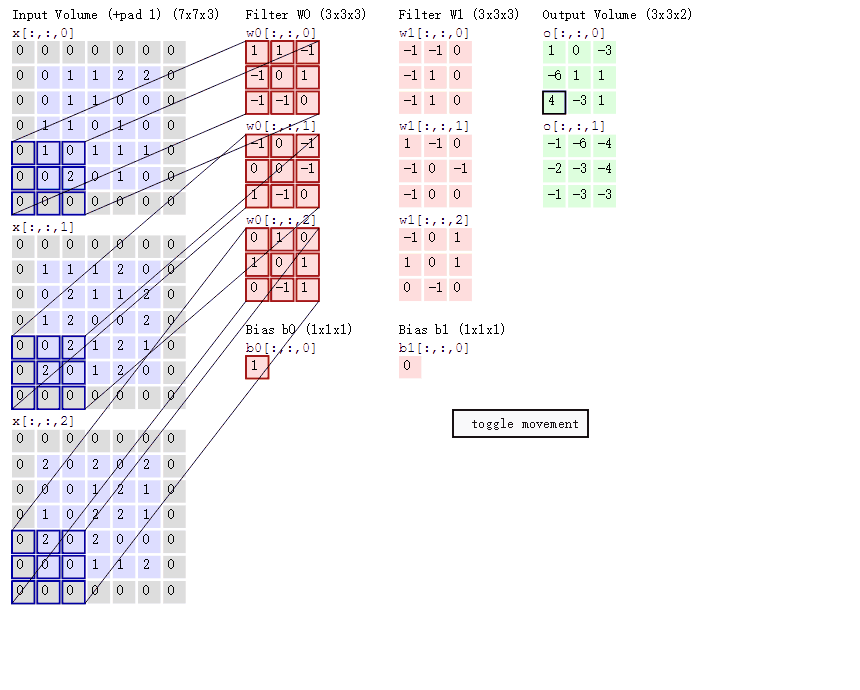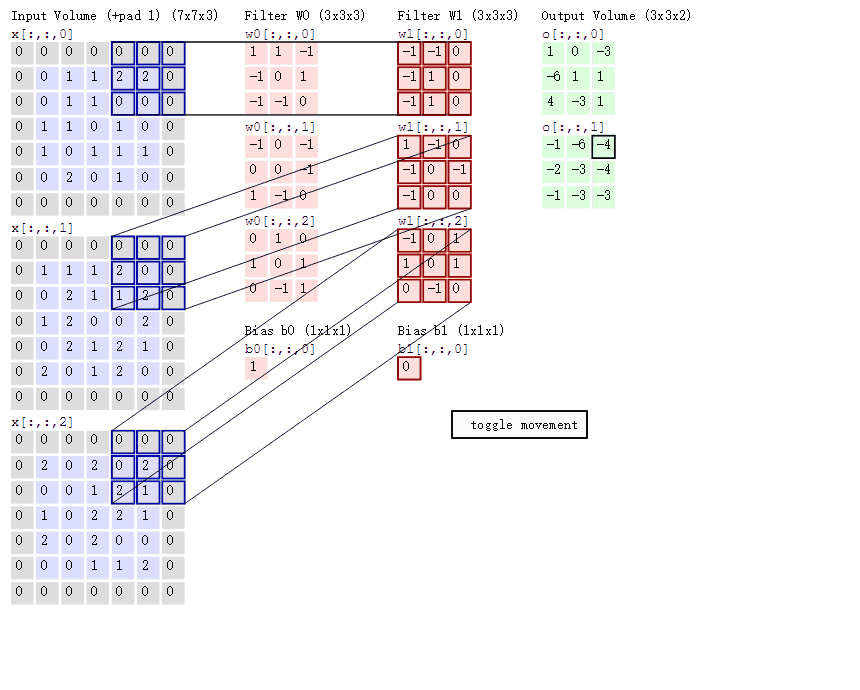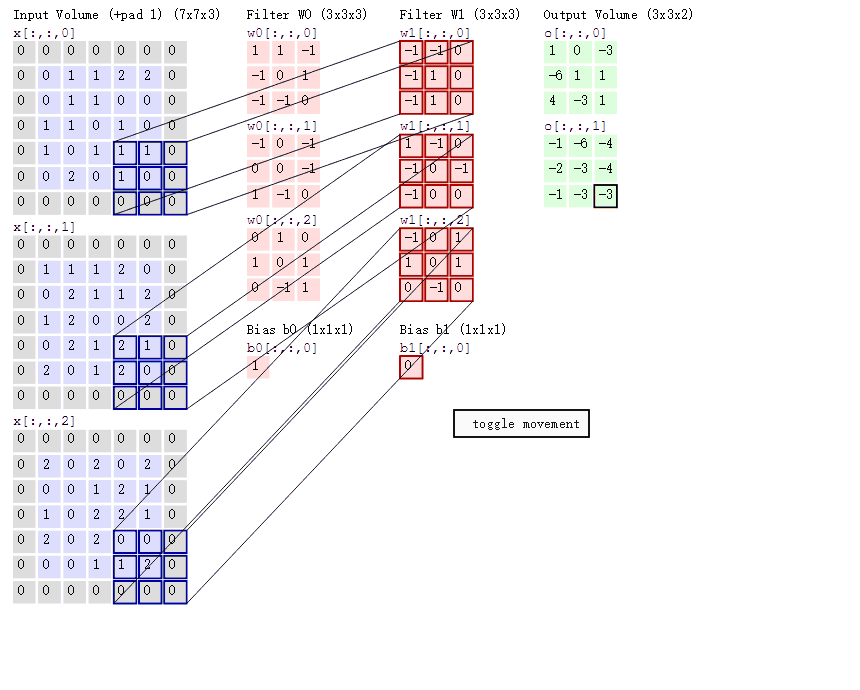
上面原图是灰度图,只有黑白两色,而彩色图像由三原色构成,二维图像在任意一个点像素为立体三层结构,分别是红色、绿色、蓝色值,该值的范围在0∽255之间,在计算机里用一个无符号的8位数表示,有三层结构彩色图像通常也称为通道数为三层,当输入图为一张3通道彩图时,也可以理解为输入3张二维图,每个二维图通道数是1,所以在CNN里‘通道数’与输入、输出时单通道图片的个数等效。下面展示是对一个三层通道彩色图像卷积过程,这个卷积过程使用了2个卷积核,用于提取图像特定的2个特征,由于图像通道数是3所以每个卷积核也是3层结构。
前面介绍了卷积可以实现降维,接下来介绍卷积如何提取图像或信号特征,图像处理中常利用二阶导数来检测图像的边缘,二维图像可以看成一个二元函数f(x,y),x和y代表像素行坐标与列坐标,函数值代表该点的像素值。在图像的边缘处一般会有颜色交替,表现为函数值一个剧烈变化,函数图如下:
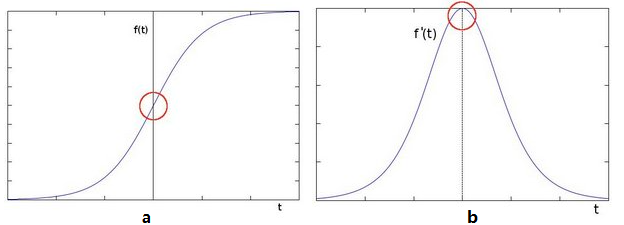
上图a前半段曲线的导数逐渐增大,在红色圆圈处导数开始变小,同时在该点导数值最大,图b显示像素值导数变化,顶端的拐点对应图a中红色标记,再对图b的函数求导即得到原图像的二阶导数如下图:
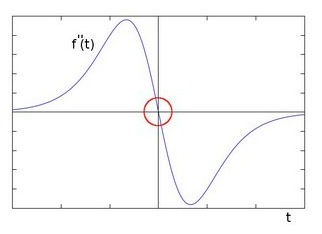
以上分析可以得出一个结论,在图像的边缘处二阶导数等于0,可以利用这个特性检测图像的边缘:首先生成一张与原图像大小一样的纯黑色图(函数值为0),然后计算每点的二阶导数并与黑色像素值相加得到一个新图片,新图片任意一点像素函数用g(x,y)表示:
g(x,y)=0+▽2f(x,y)=▽2f(x,y)
上式中▽2f(x,y)代表原图像函数的二阶导数,长*宽的二维图像可通过张量操作变成一个1*(长*宽)一维图形向量,接下来通过一维图像可推导出图像的二阶导数,一维图像导数为:
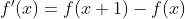
由此可以得到二阶导数:
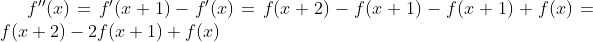
f(x+2)与f(x)中间隔了一个像素,我们希望用f(x)附近的像素来近似计算f(x)的二阶导数,上式位置参数x+2,x+1,x都顺次减一个位置可得到二阶导数近似等式(临近像素颜色值很相似,可以这样近似):
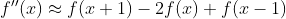 ⑤
⑤
由⑤可得到二维图像的二阶导数:
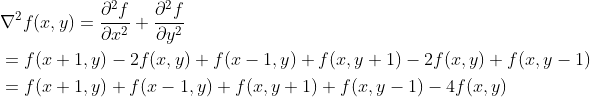 (5.1)
(5.1)
上式可以写成:

系数为0的4项:f(x-1,y-1)、f(x+1,y-1)、f(x-1,y+1)、f(x+1,y+1)分别代表f(x,y)45°方向的像素,上式代表图像与下面的卷积核做卷积运算:
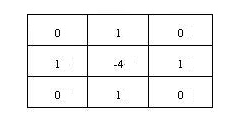
这个卷积核也称为拉普拉斯算子,根据上面的推导,用一段代码演示利用拉普拉斯算子卷积得到图像边缘的代码。
import os
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
#转化为灰度图
def rgb2gray(rgb):
return np.dot(rgb[:,:,:3], [0.299, 0.587, 0.114])
def LaplaceConvolution( ):
img = Image.open('dataset/grass.jpg')
img = np.array(img)
grayimg = rgb2gray(img)
r, c = grayimg.shape
new_image = np.zeros((r, c))
#拉普拉斯算子
L_sunnzi =np.array([[0,1,0],[1,-4,1],[0,1,0]])
for i in range(r-2):
for j in range(c-2):
#公式5.1:利用拉普拉斯算子做卷积运算
#abs取绝对值模拟Relu函数,可得到非线性输出效果
new_image[i+1, j+1] = abs(np.sum(grayimg[i:i+3, j:j+3] * L_sunnzi))
new_image=np.uint8(new_image)
plt.subplot(211)
plt.imshow(grayimg, cmap='Greys_r')
plt.subplot(212)
plt.imshow(new_image, cmap='Greys_r')
plt.show()
if __name__=='__main__':
img=LaplaceConvolution( )卷积前后的图像效果如下:

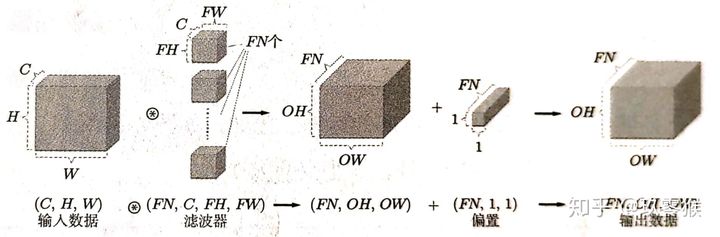
上面这个例子说明通过卷积可以获得图像的某些特征,CNN会利用多个卷积核来获得图像的多个特征,多个卷积核也称为一组滤波器。上面例子中卷积核是一个矩阵,为什么不叫卷积矩阵呢?'核'是一个立体结构,在CNN中,假设输入特征图高为H,宽度为W,通道数是C;卷积核的高为FH,宽度为FW,卷积核通道数也是C,即卷积核是一个立体结构,由C个权重矩阵复合而成,C个权重矩阵会和输入C个图全部或部分卷积相加后,得到一张通道为1的新的特征图,过程如下图:
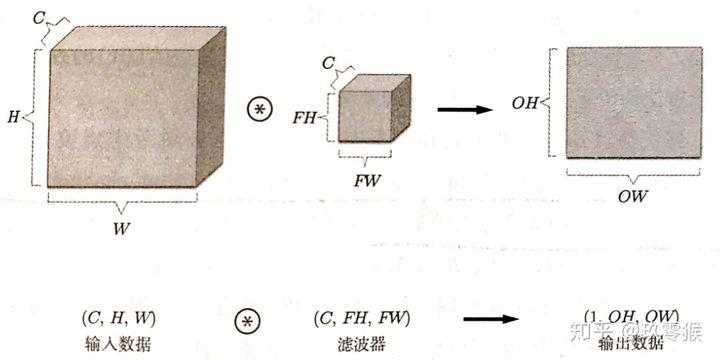
卷积需要注意两点:
1) 由于存在激活函数和Dropout机制,有些卷积核权重矩阵并没有被激活,所以卷积核会与上层输入C个图像部分卷积而不是全部。
2) 无论输入图片通道数是多少,卷积后每个特征图通道数都是1,卷积后的每个特征图带有所有或部分上层输入图的特征信息,且输出特征图的个数与卷积核个数相关,有几个卷积核就有几个输出图,称输出特征图的个数为卷积层的通道数、或卷积核的个数,这两个都是一个概念。
当有多个卷积核时卷积层输出图也是一个立体结构,下图卷积层有FN个卷积核,输出图像维度是OW*OH*FN,需要注意的是上层特征图与卷积核卷积后一般会加上一个偏置项,而每个卷积核偏置项都是一样的,即有FN个卷积核同时就有FN个偏置项:
1.2 池化层
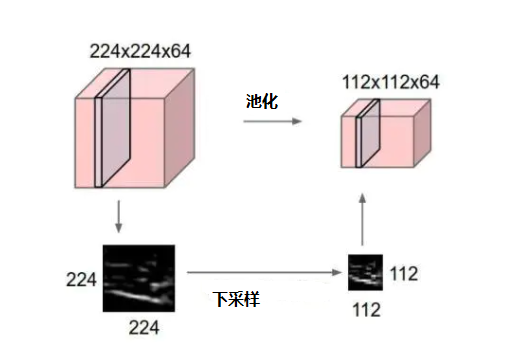
池化(pooling)层是将卷积后的特征图进一步降维、缩小特征图尺寸,池化后对信息是虽然有损失的,但也保证了模型有较好的拟合能力,常见池化示意图如下:
常用池化手段有最大池化法(Max pooling)、平均池化法(Average pooling),最大池化法取池化窗口内最大值作为输出,过程如下图所示:
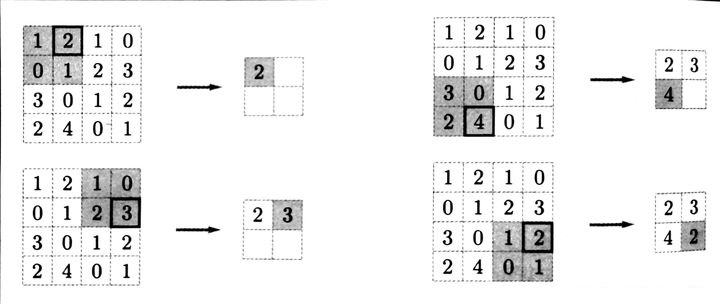
上图最大值池化法池化窗口为2*2,步长为2,平均池化法则取池化窗口内平均值作为输出。需要注意:当使用最大池化法时要同时记下池化窗口内最大值的位置,在反向传播时,最大值处有相应的梯度值,而在非最大值出梯度为0;另外,池化层没有使用激活函数,池化层输入等于输出。
二、卷积神经网络的反向传播
卷积神经网络概念最早在80年代就由日本学者福岛邦彦提出,当时借鉴了动物的视觉皮层命名为neocognitron,早期的卷积神经网络并未引入局部感受野、权值共享、反向传播等理念,导致卷积神经网络在识别率上一度被SVM这类感知机吊打,直到Yann LeCun引入现代神经网络技术后CNN才实现了与人类不相上下的识别率,了解CNN反向传播有助于了解其他衍生的卷积神经网络模型如ResNet、GooLeNet、AlexNet等。
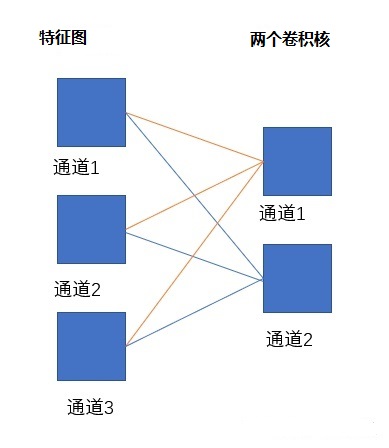
CNN与全连接神经网络一样,损失函数的误差在层与层之间传递,在接下来的章节中还会了解到,有些神经网络模型如循环神经网络(RNN),长短时记忆网络(LSTM)不仅有层与层之间的误差传递,还有时间维度上的误差。CNN卷积过程也可以表达成全连接神经网络类似的方式,下图是三个特征图经过两个卷积核滤波的情形,与全连接神经网络区别是下图中连线代表卷积,每个连线上式卷积核中对应的一个权重矩阵:
反向传播时,假设目前层为l,该层的输入为zl,输出为al,两者关系为:al=σ(zl),σ表示为激活函数,CNN在卷积层常用的激活函数是Relu函数,在之前介绍过:Relu(x)=max{0,x},当x大于0时,Relu函数的导数为1。在神经网络的反向传播中,利用链式法则求任意一层的误差时,需要一直定位到该层的输入端,用公式可表达为:
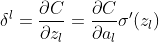
上式中C代表损失函数,在分类问题中常用softmax函数实现的交叉熵作为损失函数,接下来分三种情况讨论CNN的反向传播。
2.1、已知池化层δl,求上一层δl-1
| 上一篇 DNN-全连接神经网络 | 下一篇 RNN-循环神经网络(上) |
| 评论区 | |