Apriori算法、朴素贝叶斯分类
概率学分为古典概率学派和贝叶斯学派两大学派,古典概率学派认为一个事件发生的频率等于其概率,这在许多场合下是正确的,根据大数定律事件发生的频率依概率收敛于一个数值,古典概率学派认为概率是一个具体数值,比如扔一枚硬币在次数足够多的情况下,硬币为反面的概率等于硬币为正面频率;而贝叶斯学派认为概率是一个分布,这个分布依赖于观察值而变化。打一个比方,想知道某人创业是否能成功时,频率派会说有可能失败也有可能成功,一半一半(50%)吧,而贝叶斯派则会根据现有的数据或主观感受,比如说目前创业能获得成功的大概30%-40%左右,或者认为现在行情比较好认为成功的概率80%以上,这个期初主观估计在贝叶斯学派称为先验概率,但如果这个人爸爸是马云呢,那成功率就是100%了吧,即后期的观察值会改变先验概率,由观察值调整后的概率称为后验概率。
贝叶斯学派最大的争议在于先验概率带有主观性,比如想知道一个人三分球的命中率,贝叶斯学派可以拿现在NBA球员命中率比如33%作为先验概率,甚至也可以是100%=1/1或者是0都可以作为先验概率,随后让这个人投篮计算命中率,投一次分母加1,命中一次分子加1,当次数足够多时,这个命中率会稳定在一个数值。这就是贝叶斯派特征,先设定一个先验概率然后通过观察数据确定后验概率,后验概率也叫条件概率。

本篇将介绍两种算法,Apriori算法假设各个随机变量不独立,需要计算各个随机变量之间的关联性;朴素贝叶斯分类则默认随机变量之间独立,利用联合密度分布进行分类。这两种算法是数据挖掘的常用算法,功能实现也比较简单。
一、Apriori算法
假设有基本事件A1,A2,A3,...,An,如果有P(Ai|Aj)>P(Ai),则称Aj对Ai有提升作用,也称Aj,Ai是相互关联的,这里也可以是复合事件比如有P(A2,A3|A4,A5)>P(A2,A3),则认为A4,A5对A2,A3有提升作用。A2,A3复合事件称为一个项集,有两个基本事件复合而成是一个二项集,类似的有一项集,K项集等。
一个项集发生的概率称为这个项集的支持度,从上面分析可以知道支持度是一个联合概率,可以先预先设置一个支持度数值,如果项集的支持度大于等于这个支持度则称这个项集为频繁项集。一个项集的支持度高不一定代表其概率值高,但项集概率值高其支持度一定高。
对于一项集而言P(Ai|Aj)称为Aj →Ai的置信度,从上面分析可以知道置信度是一个条件概率值,而Lift(Aj →Ai) = P(Ai|Aj)/ P(Ai)称为Aj →Ai的提升度,当提升度大于1时认为Aj 对Ai 有提升作用,提升度小于1时认为Aj 对Ai 有抑制作用,而等于1时则认为Aj 和Ai 独立不相关,将置信度和提升度可以拓展到多项集上。
Apriori算法主要分为两步:
第一步:先设置一个支持度阈值,找出各个项集的频繁项集。
第二步:将各个频繁项集两两组合分别计算提升度,找出项集之间的关联性。
Apriori算法比较简单,按照以上介绍应该可以很轻松的写出代码,本篇不提供Apriori算法示例代码了,这里只展示一个Apriori算法过程,下面的组图是一个餐厅订餐的案例,设置支持度阈值为20%:
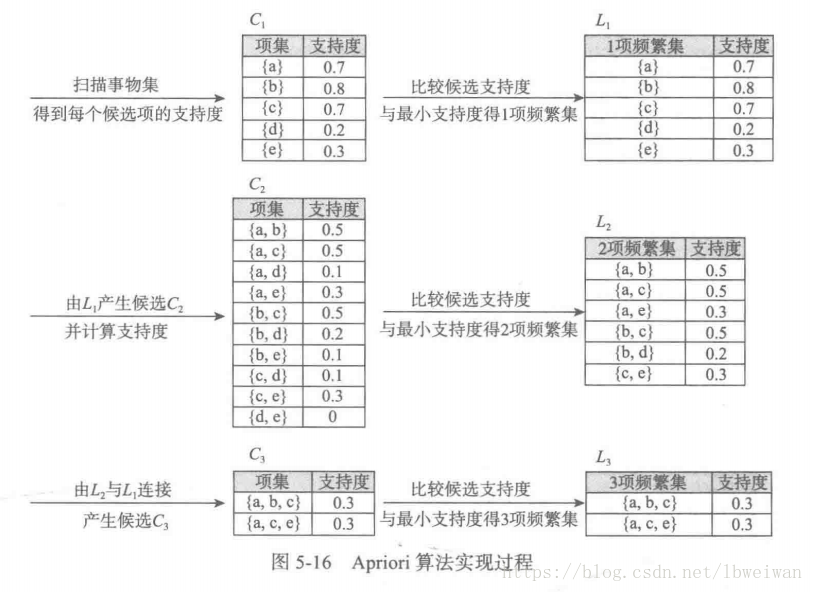

以a->b为例,p(a,b)概率为0.5,所以a,b项集的支持度Support为50%;而置信度Confidence:p(b|a)=p(a,b)/p(a)=0.5/0.7=0.71428,其他数据都可按此计算。
一、朴素贝叶斯分类
与Apriori算法一样,朴素贝叶斯也是利用联合分布函数生成条件概率进行分类,之前已经说明过朴素贝叶斯有一个独立性的假设,即事件Ai,Aj,Ak两两独立则有P(Ai,Aj,Ak)=P(Ai)P(Aj)P(Ak),朴素贝叶斯具体算法过程可以如下描述:


有了上面介绍后来具体看一个例子,这是一个由历史病例来判断病人病症的案例,现有以下这张历史病历表:

上表中感冒、过敏、脑震荡是分类,症状和职业为属性。现有一个建筑工人有打喷嚏的症状,需要判断得那种疾病的概率最大,从上面可以看到按疾病结果分类看有三类,其概率分别为P(感冒)=50%,P(过敏)=17%,P(脑震荡)=33%,而按职业属性分类有下表:
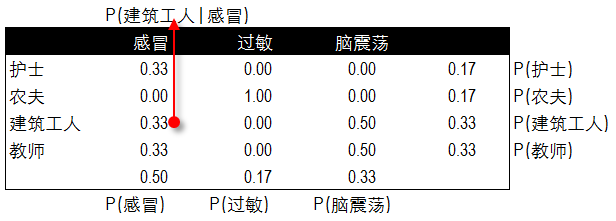
上表中P(建筑工人|感冒)=患感冒建筑工人/感冒的数量=1/3=0.33,其他数字按此计算。而按病人症状属性可以有下张表:
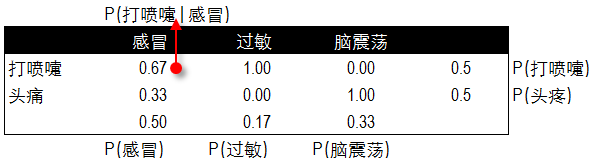
代入之前公式知对于各个疾病有以下参考量
当分类感冒时:P(建筑工人|感冒)*P(打喷嚏|感冒)*P(感冒)=0.33*0.67*0.5=0.11055
当分类过敏时:P(建筑工人|过敏)*P(打喷嚏|过敏)*P(过敏)=0*1*0.17=0
当分类脑震荡时:P(建筑工人|脑震荡)*P(打喷嚏|脑震荡)*P(脑震荡)=0.5*0*0.33=0
利用朴素贝叶斯可以知道一个建筑工人打喷嚏可能是感冒了。
| 上一篇 隐马尔科夫链HMM详解 | 下一篇 利用线性空间、子空间实现线性回归问题 |
| 评论区 | |