决策树(上)-ID3与C4.5
决策树是利用可视化的树结构实现数据的分类或回归,现实中分类比如银行根据收入、职业、婚姻状况、年龄等属性了解客户的贷款是否能按期偿还,其分类为“是”或“否”,再比如过安检时,根据旅客脸部数据分类为是否是通缉人员;回归则是为了得到具体数值,比如根据年龄、身高、性别得到目标数据的体重。决策树是一种监督学习过程,利用已经标记的数据生成树模型。依照决策树发展历程先后有ID3,C4.5和CART(Classification and Regression Trees),其中ID3、C4.5的提出者都是一个人,C4.5是对ID3的改进,ID3、C4.5其核心理论基础是之前介绍的信息熵,CART是一个能同时实现分类和回归的二叉树模型,本篇将重点介绍C4.5。
一、ID3
ID3和C4.5都只能解决分类问题,ID3是利用信息熵熵实现的决策树,关于熵的知识请看信息熵、交叉熵、相对熵原理与softmax函数的应用。ID3算法是首先计算样本总体信息熵,然后依次计算每个属性的条件熵,条件熵越小说明该属性对于降低分类是有益的,可以作为分类的结点,或者用信息熵减去条件熵得到信息增益,信息增益越大的属性作为决策树的结点,条件熵小和信息增益大表达是同一个意思,具体计算过程如下:

ID3优先选择值较多属性作为分类结点,这带来一些其他的问题:比如属性值不是离散型而是连续型的数值时,如果将连续值做离散化处理后会造成该属性的值非常多,造成在ID3的算法会优先选择数值型属性进行分类,因此,ID3只能处理属性值为离散型的分类。实践中很少利用ID3进行分类,本篇不做详细介绍。虽然ID3没有太大的应用价值,但可以'抛砖引玉'通过ID3的引出c4.5,c4.5改进了ID3算法,解决了ID3算法不足,c4.5能解决属性值是连续型的分类问题。
二 、C4.5
ID3喜欢属性值多样化的属性作为决策树分裂结点,结合之前信息熵的知识可以了解到,属性值多的属性其本身的熵也大,如果将信息增益除以属性本身的熵,将属性的熵作为一个惩罚性因子,就可以抵消因为属性值多而带来的选择优势。C4.5正是基于这种思维获得很好的效果,只是在ID3基础上稍微变动了一下,让C4.5长期以来雄霸数据挖掘算法排行榜第一。

2.1 C4.5树分类与剪枝
下面是一个利用C4.5实现鸢尾花数据分类例子,这个数据集在介绍PCA时使用过,鸢尾花数据可以分为三类,分别是山鸢尾 ,北美鸢尾,变色鸢尾,鸢尾花具有4个属性,分别是花萼的长度、花萼的宽度、花瓣的长度,花瓣的宽度,可以发现这个例子中属性都是连续的数值型。C4.5的实现不算复杂,但是需要注意决策树在生成后一定要做剪枝以避免‘过拟合’现象,这里打上粗体表明重要性,没有经过剪枝的决策树是没有实用意义的。
==treePlot.py== 显示C4.5决策树工具类
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
decisionNode = dict(boxstyle='sawtooth', fc='0.8')
leafNode = dict(boxstyle='round4', fc='0.8')
arrow_args = dict(arrowstyle='<-')
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va='center', ha='center', bbox=nodeType,
arrowprops=arrow_args)
# 获取叶子节点数目和树的层数
def getNumLeafs(myTree):
numLeafs = 0
firstStr =list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if (type(secondDict[key]).__name__ == 'dict'):
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if (type(secondDict[key]).__name__ == 'dict'):
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotTree(myTree, parentPt, nodeTxt): # if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) # this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys()) [0] # the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key], cntrPt, str(key)) # recursion
else: # it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
# fig.title("c4.5",size=14)
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks
#createPlot.ax1.set_title("c4.5", size=24)
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0;
plotTree(inTree, (0.5, 1.0), '')
plt.show()==c45.py== c4.5决策树实现代码:
# coding=utf-8
import math
import operator
from sklearn import datasets
from treePlot import *
#加载数据集
def createDataSet_iris():
iris = datasets.load_iris()
dataSet = []
for var in iris.data:
dataSet.append(list(var))
targets = iris.target
for index, var in enumerate(targets):
dataSet[index].append(var)
labels = ['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度']
return dataSet,labels
##计算给定数据集的信息熵
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): # 为所有可能分类创建字典
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries
shannonEnt -= prob * math.log(prob, 2) # 以2为底数求对数
return shannonEnt
# 依据特征划分数据集 axis代表第几个特征 value代表该特征所对应的值 返回的是划分后的数据集
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis + 1:])
retDataSet.append(reducedFeatVec)
return retDataSet
# 选择信息增益比最大属性作为分裂节点
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征个数
baseEntropy = calcShannonEnt(dataSet)
bestInfoGainrate = 0.0
bestFeature = -1
for i in range(numFeatures): # 遍历特征 第i个
featureSet = set([example[i] for example in dataSet]) # 第i个特征取值集合
newEntropy = 0.0
splitinfo = 0.0
for value in featureSet:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet) # 该特征划分所对应的entropy
splitinfo -= prob * math.log(prob, 2)
if not splitinfo:
splitinfo = -0.99 * math.log(0.99, 2) - 0.01 * math.log(0.01, 2)
infoGain = baseEntropy - newEntropy
infoGainrate = float(infoGain) / float(splitinfo)#信息增益比
if infoGainrate > bestInfoGainrate:
bestInfoGainrate = infoGainrate
bestFeature = i
return bestFeature
# 创建树的函数代码 python中用字典类型来存储树的结构 返回的结果是myTree-字典
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
# 类别完全相同则停止继续划分 返回类标签-叶子节点
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList) # 遍历完所有的特征时返回出现次数最多的
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel: {}}
del (labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet] # 得到的列表包含所有的属性值
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
return myTree
# 多数表决的方法决定叶子节点的分类 ---- 当所有的特征全部用完时仍属于多类
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0;
classCount[vote] += 1
# 排序函数 operator中的
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
# 自底向上剪枝
def prune_downtoup(inputTree, dataSet, featLabels, count):
# global num
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
for key in secondDict.keys(): # 走到最深的非叶子结点
if type(secondDict[key]).__name__ == 'dict':
tempcount = [] # 本将的记录
rightcount = 0
wrongcount = 0
tempfeatLabels = featLabels[:]
subDataSet = splitDataSet(dataSet, featIndex, key)
tempfeatLabels.remove(firstStr)
getCount(secondDict[key], subDataSet, tempfeatLabels, tempcount)
tempnum = 0.0
wrongnum = 0.0
old = 0.0
# 标准误差
standwrong = 0.0
for var in tempcount:
tempnum += var[0] + var[1]
wrongnum += var[1]
old = float(wrongnum + 0.5 * len(tempcount)) / float(tempnum)
standwrong = math.sqrt(tempnum * old * (1 - old))
# 假如剪枝
new = float(wrongnum + 0.5) / float(tempnum)
if tempnum*new <= tempnum*old + standwrong : # 要确定新叶子结点的类别
# 误判率最低的叶子节点的类为新叶子结点的类
# 在count的每一个列表类型的元素里再加一个标记类别的元素。
wrongtemp = 1.0
newtype = -1
for var in tempcount:
if float(var[1] + 0.5) / float(var[0] + var[1]) < wrongtemp:
wrongtemp = float(var[1] + 0.5) / float(var[0] + var[1])
newtype = var[-1]
secondDict[key] = str(newtype)
tempcount = [] # 这个相当复杂,因为如果发生剪枝,才会将它置空,如果不发生剪枝,那么应该保持原来的叶子结点的结构
for var in tempcount:
count.append(var)
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
continue
rightcount = 0
wrongcount = 0
subDataSet = splitDataSet(dataSet, featIndex, key)
for eachdata in subDataSet:
if str(eachdata[-1]) == str(secondDict[key]):
rightcount += 1
else:
wrongcount += 1
count.append([rightcount, wrongcount, secondDict[key]]) # 最后一个为该叶子结点的类别
#计算任意子树正确率
def getCount(inputTree, dataSet, featLabels, count):
# global num
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
# count=[]
for key in secondDict.keys():
rightcount = 0
wrongcount = 0
tempfeatLabels = featLabels[:]
subDataSet = splitDataSet(dataSet, featIndex, key)
tempfeatLabels.remove(firstStr)
if type(secondDict[key]).__name__ == 'dict':
# 如果是子树结点,递归调用
getCount(secondDict[key], subDataSet, tempfeatLabels, count)
else:
for eachdata in subDataSet:
if str(eachdata[-1]) == str(secondDict[key]):
rightcount += 1
else:
wrongcount += 1
count.append([rightcount, wrongcount, secondDict[key]])
# num+=rightcount+wrongcount
# 自顶向下剪枝
def prune_uptodown(inputTree, dataSet, featLabels):
firstStr = list(inputTree.keys()) [0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
#如果是子树则计算该结点错误率
tempfeatLabels = featLabels[:]
subDataSet = splitDataSet(dataSet, featIndex, key)
tempfeatLabels.remove(firstStr)
tempcount = []
#tempcount保存了所有子树结点正确与错误的个数、以及该子树对应分裂属性
getCount(secondDict[key], subDataSet, tempfeatLabels, tempcount)
tempnum,wrongnum,standwrong = 0.0,0.0,0.0
for var in tempcount:
tempnum += var[0] + var[1]
wrongnum += var[1]
treeErr = float(wrongnum + 0.5 * len(tempcount)) / float(tempnum)
standwrong = math.sqrt(tempnum * treeErr * (1 - treeErr))#方差
# 如果用叶结点代替子树结点
nodeErr = float(wrongnum + 0.5) / float(tempnum)
#判断条件对应公式(2.4)
if tempnum*nodeErr <= tempnum*treeErr + standwrong : # 要确定新叶子结点的类别
# 误判率最低的叶子节点的类为新叶子结点的类
# 在count的每一个列表类型的元素里再加一个标记类别的元素。
#print(key,old,new)
wrongtemp = 1.0
newtype = -1
for var in tempcount:
if float(var[1] + 0.5) / float(var[0] + var[1]) < wrongtemp:
wrongtemp = float(var[1] + 0.5) / float(var[0] + var[1])
newtype = var[-1]
secondDict[key] = str(newtype)
def getsortNum(mapfeatures,num):
if num<mapfeatures[0] or num > mapfeatures[len(mapfeatures) - 1] :
return num
for i in range(len(mapfeatures) - 1):
if (num > mapfeatures[i] and num <= mapfeatures[i + 1]):
return mapfeatures[i + 1]
#处理连续型属性
def handleContinuousNumber(dataset,index ):
features=set(data[index] for data in dataset[:])
sortfeatures=sorted( features)
mapfeatures=[]
for i in range(len(sortfeatures)-1):
mapfeatures.append( round ((sortfeatures[i]+sortfeatures[i+1])/2 ,2) )
for i in range(len(dataset)):
dataset[i][index]=getsortNum(mapfeatures,dataset[i][index])
if __name__ == '__main__':
global num
num = 0
dataset, features = createDataSet_iris()
for a in range(len(features)):
handleContinuousNumber(dataset[:], a)#1
features4uptodown= features.copy()
tree = createTree(dataset, features)#2
createPlot(tree)
#自顶向下剪枝
prune_uptodown(tree, dataset, features4uptodown )#3
createPlot(tree)
#自低向上剪枝
'''
features4downtoup = features.copy()
count = []
cutBranch_downtoup(tree, dataset, features4downtoup, count)
createPlot(tree)
'''程序说明:
1#:handleContinuousNumber(dataset[:], a) :处理连续数值型属性,加载数据后排序,将排序好数组相邻两个元素取平均值,新生成的序列将属性值划分为149个区间(原来有150个数据),依次将4个属性做离散化处理。
2# tree = createTree(dataset, features)根据公式(1.5)生成决策树,实现此功能的函数是chooseBestFeatureToSplit,chooseBestFeatureToSplit函数是利用信息增益比选择最佳的属性作为决策树的节点。
3#prune_uptodown(tree, dataset, features4uptodown ),这里采用悲观算法实现从顶向下剪枝,没有剪枝前决策树如下图:
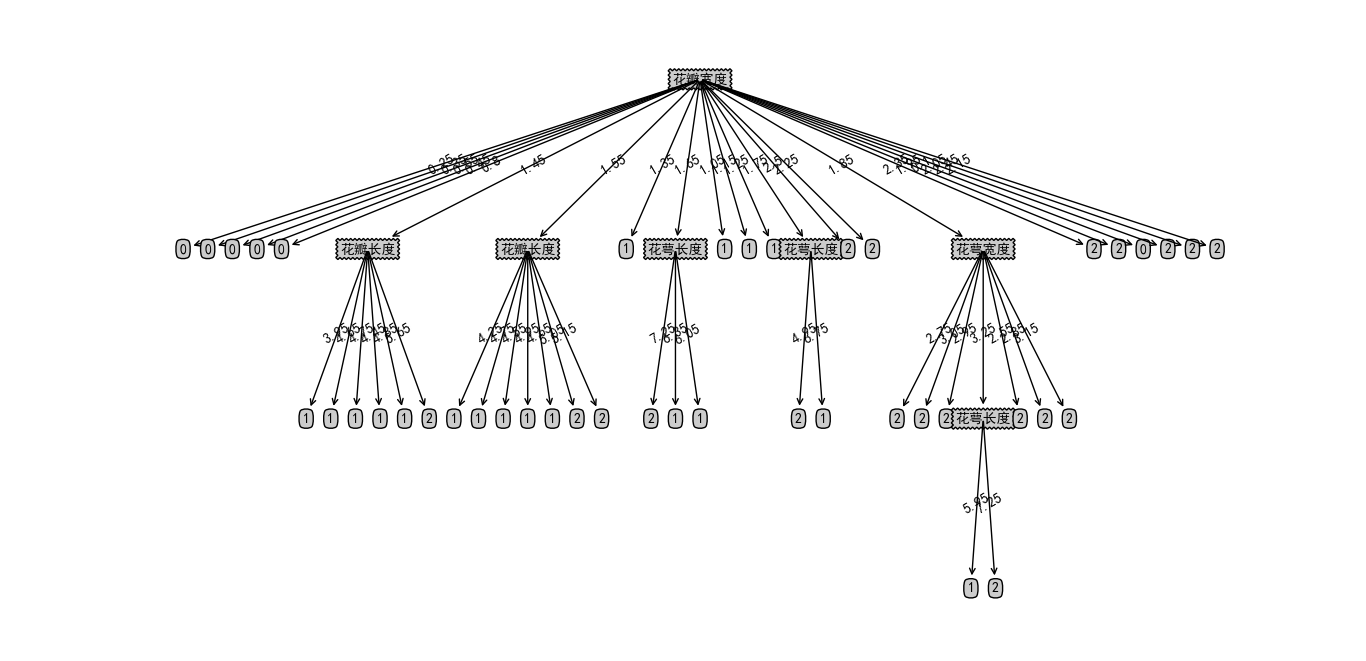
剪枝后发现,根据花瓣宽度属性就可以实现分类,如下图所示:
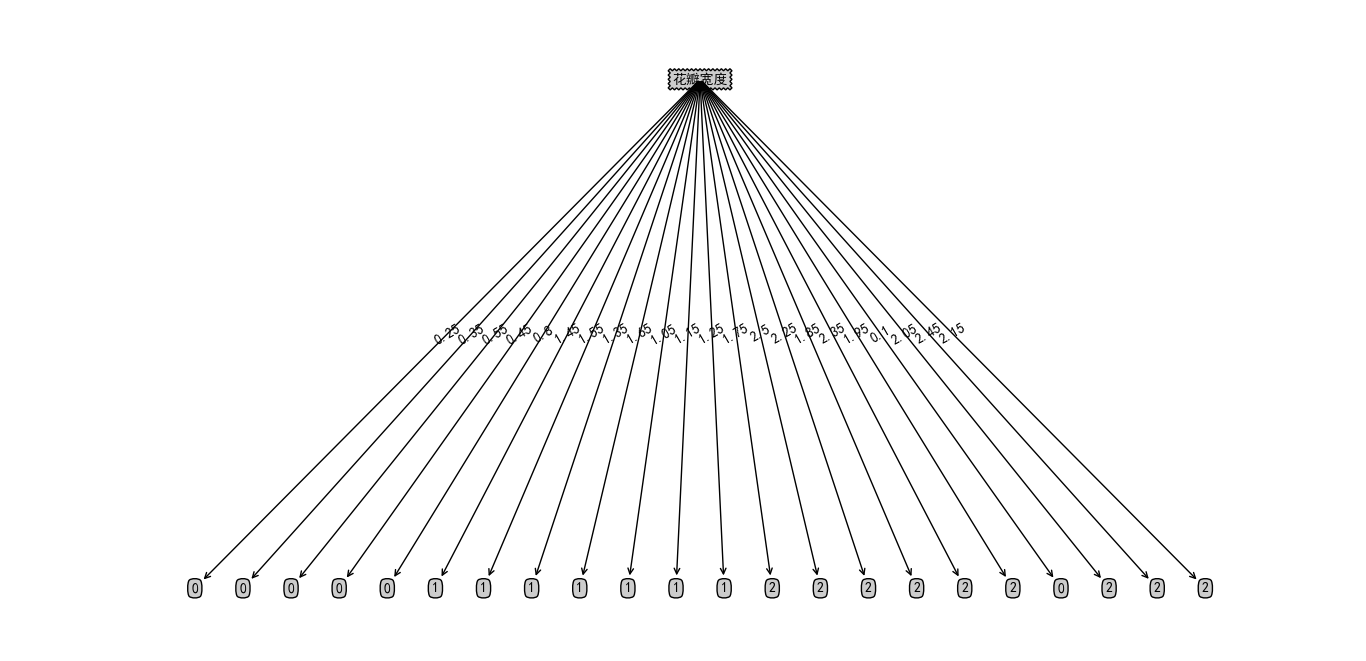
2.2 C4.5剪枝
| 上一篇 信息熵、交叉熵、相对熵原理与softmax函数的应用 | 下一篇 决策树(下)-CART树分类、回归、剪枝实现 |
| 评论区 | |